Question

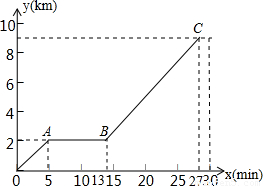
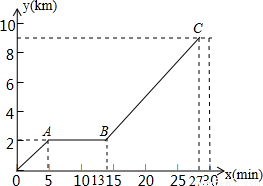
甲、乙两位同学住在同一小区，在同一中学读书，一天恰好在同一时间骑自行车沿同一线路上学，小区离学校有9km，甲以匀速行驶，花了30min到校，乙的行程信息如图中折线O-A-B-C所示，分别用y₁，y₂表示甲、乙在时间x（min）时的行程，请回答下列问题：
（1）分别用含x的解析式表示y₁，y₂（标明x的范围），并在图中画出函数y₁的图象；
（2）甲、乙两人在途中有几次相遇？分别是出发后的多长时间相遇？

Answer 1

分析：（1）小区离学校有9km，甲以匀速行驶，花了30min到校，故y₁行程与时间的函数关系式是正比例函数．由图形可以看出y₂图象由三部分组成，写出该定义域各个函数关系式．
（2）若要途中相遇，则路程相等，联合函数解析式解出交点，就能求出时间．

解答：解：（1）∵小区离学校有9km，甲以匀速行驶，花了30min到校，
∴y1=

3

10

x(0≤x≤30)，其中甲的图象为线段OD，
∵A（5，2），B（13，2），C（27，9），
∴利用待定系数法得
y₂=

2 5 x       (0≤x＜5) 2          (5≤x＜13) 1 2 x- 9 2  (13≤x≤27)

，
当5≤x≤13，y₂=2；

（2）由

y=2 y= 3 10 x

得x=

20

3

，
由

y= 3 10 x y= 1 2 x- 9 2

得x=

45

2

，
∴甲，乙在途中有两次相遇，相遇时间分别为出发后6分40秒，22分30秒．

点评：本题主要考查一次函数的应用，由图象写出函数解析式，联合函数解析式求出交点．