Question

在正方形ABCD中，对角线AC、BD交于点O，AC=2，PE⊥OA于E，PF⊥OB于F，则PE+PF=________．

Answer 1

分析：正方形对角线AC、BD交于点O，根据PE⊥AC，BD⊥AC可以证明PE∥BD，则=，同理=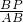，利用AP+BP=AB，AO=BO得出PE+PF=AO=BO．
解答：解：∵PE⊥AC，BD⊥AC
∴PE∥BO，
∴△APE∽△ABO，
∴=，
同理可证：=，
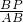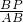∴+=+==1，
∵AO=BO，∴PE+PF=AO=BO，
∵AC=2，∴AO=，
故PE+PF=，
故答案为：．
点评：本题考查了正方形各边相等，且各内角为直角的性质以及相似三角形对应边的比值相等，本题中正确的根据AO=BO化简+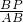=+==1是解题的关键．