Question

【题目】图a、图b是两张形状、大小完全相同的方格纸，方格纸中每个小正方形的边长为1，点A、B、D在小正方形的顶点上．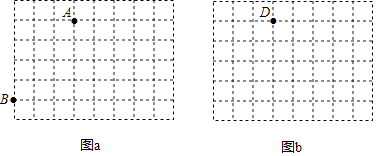

（1）在图a中画出△ABC（点C在小正方形顶点上），使△ABC是等腰三角形，且∠ABC=45°；
（2）在图b中画出△DEF（E、F在小正方形顶点上），使△DEF∽ABC且相似比为1： ．

Answer 1

【答案】
（1）解：如图a

（2）如图b

【解析】（1）根据题意画出等腰三角形；（2）根据图a，按比例画出图b．
【考点精析】掌握等腰三角形的判定和勾股定理的概念是解答本题的根本，需要知道如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．