题目内容
（1）猜想在锐角三角形ABC中，cosA+cosB+cosC与sinA+sinB+sinC的大小关系如何，并验证你的猜想；
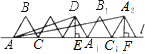
（2）如图所示，已知边长是2a的正三角形ABC沿直线L滚动，你能设法求出∠DAC+∠A2AC的度
数吗？不妨试一试．
（2）如图所示，已知边长是2a的正三角形ABC沿直线L滚动，你能设法求出∠DAC+∠A2AC的度
数吗？不妨试一试．
（1）猜想：cosA+cosB+cosC＜sinA+sinB+sinC．
验证：如∠A=50°，∠B=60°，∠C=70°时，
cosA+cosB+cosC≈1.485，而sinA+sinB+sinC≈2.572，
故成立；
（2）过点D作DE⊥L于点E，过点A2作A2F⊥L于点F，
∴tan∠DAC=
=
=
，tan∠A2AC=
=
=
．
∴∠DAC≈19.1°，∠A2AC≈10.9°．
故∠DAC+∠A2AC=19.1°+10.9°=30°．
验证：如∠A=50°，∠B=60°，∠C=70°时，
cosA+cosB+cosC≈1.485，而sinA+sinB+sinC≈2.572，
故成立；
（2）过点D作DE⊥L于点E，过点A2作A2F⊥L于点F，
∴tan∠DAC=
| DE |
| AE |
| ||
| 5a |
| ||
| 5 |
| A2F |
| AF |
| ||
| 9a |
| ||
| 9 |
∴∠DAC≈19.1°，∠A2AC≈10.9°．
故∠DAC+∠A2AC=19.1°+10.9°=30°．
练习册系列答案
相关题目
数吗？不妨试一试．
数吗？不妨试一试．
