题目内容
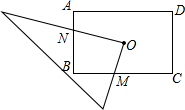
如图所示，O为矩形ABCD的对称中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与BC、AB相交，交点分别为M、N．如果AB=6，AD=8，OM=x，ON=y，则y与x的关系是________（不填x的取值范围）
y=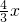
分析：作OP垂直AB于点P，OQ垂直BC于点Q．可证△ONP∽△OQM，根据相似三角形的性质求解．
解答：
解：作OP垂直AB于点P，OQ垂直BC于点Q．
∵∠PON+∠POM=90°，∠POM+∠MOQ=90°，
∴∠PON=∠MOQ，∠NPO=∠MQO，
∴△ONP∽△OQM，
OP：OQ=
=ON：OM．
所以y=
x．
故答案为y=x．
点评：此题主要考查了矩形的性质，旋转的性质，相似三角形的性质，解决本题的关键是根据相似得到相应的等量关系．注意利用矩形的一些性质．
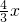
分析：作OP垂直AB于点P，OQ垂直BC于点Q．可证△ONP∽△OQM，根据相似三角形的性质求解．
解答：
解：作OP垂直AB于点P，OQ垂直BC于点Q．∵∠PON+∠POM=90°，∠POM+∠MOQ=90°，
∴∠PON=∠MOQ，∠NPO=∠MQO，
∴△ONP∽△OQM，
OP：OQ=
=ON：OM．所以y=
x．故答案为y=
x．点评：此题主要考查了矩形的性质，旋转的性质，相似三角形的性质，解决本题的关键是根据相似得到相应的等量关系．注意利用矩形的一些性质．
练习册系列答案
相关题目
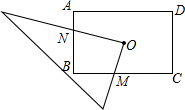如图所示，O为矩形ABCD的对称中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与BC、AB相交，交点分别为M、N．如果AB=6，AD=8，OM=x，ON=y，则y与x的关系是
