题目内容
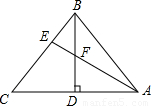
 已知:BD为△ABC边AC上的高,E为BC上一点,CE=2BE,∠CAE=30°,若EF=3,BF=4,则AF的长为________.
已知:BD为△ABC边AC上的高,E为BC上一点,CE=2BE,∠CAE=30°,若EF=3,BF=4,则AF的长为________.
7
分析:过E作EM⊥BD于M,求出∠DFA=60°=∠EFM,求出∠MEF,根据EF=3,求出EM、FM,求出BM,根据勾股定理求出BE、求出BC,根据cos∠CBD求出DB,求出FD,根据含30度角的直角三角形性质求出即可.
解答: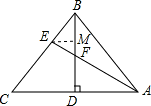 过E作EM⊥BD于M,则∠BME=∠FME=90°,
过E作EM⊥BD于M,则∠BME=∠FME=90°,
∵∠CAE=30°,∠BDA=90°,
∴∠AFD=60°=∠EFM,
∴∠MEF=30°,
∵EF=3,
∴MF= ,
,
由勾股定理得:EM=
 ,
,
∵BF=4,
∴BM=4- =
= ,
,
在△BEM中,由勾股定理得:BE=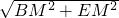 =
= ,
,
∵CE=2BE,
∴BC=3 ,
,
∵cos∠CBD= =
=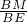 =
=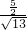 ,
,
∴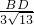 =
=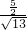 ,
,
BD= ,
,
∴DF=BD-BF= -4=
-4= ,
,
∵∠FDA=90°,∠FAD=30°,
∴AF=2DF=7.
故答案为:7.
点评:本题考查了解直角三角形,勾股定理,含30度角的直角三角形等知识点,主要考查学生综合运用性质进行计算的能力,题目比较好,但是有一定的难度.
分析:过E作EM⊥BD于M,求出∠DFA=60°=∠EFM,求出∠MEF,根据EF=3,求出EM、FM,求出BM,根据勾股定理求出BE、求出BC,根据cos∠CBD求出DB,求出FD,根据含30度角的直角三角形性质求出即可.
解答:
 过E作EM⊥BD于M,则∠BME=∠FME=90°,
过E作EM⊥BD于M,则∠BME=∠FME=90°,∵∠CAE=30°,∠BDA=90°,
∴∠AFD=60°=∠EFM,
∴∠MEF=30°,
∵EF=3,
∴MF=
 ,
,由勾股定理得:EM=

 ,
,∵BF=4,
∴BM=4-
 =
= ,
,在△BEM中,由勾股定理得:BE=
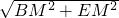 =
= ,
,∵CE=2BE,
∴BC=3
 ,
,∵cos∠CBD=
 =
=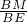 =
=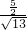 ,
,∴
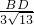 =
=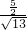 ,
,BD=
 ,
,∴DF=BD-BF=
 -4=
-4= ,
,∵∠FDA=90°,∠FAD=30°,
∴AF=2DF=7.
故答案为:7.
点评:本题考查了解直角三角形,勾股定理,含30度角的直角三角形等知识点,主要考查学生综合运用性质进行计算的能力,题目比较好,但是有一定的难度.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
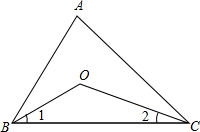
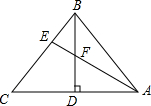 (2012•南岗区二模)已知:BD为△ABC边AC上的高,E为BC上一点,CE=2BE,∠CAE=30°,若EF=3,BF=4,则AF的长为
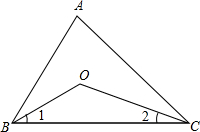
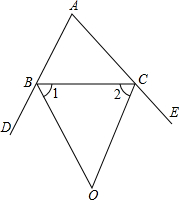
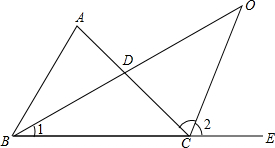
(2012•南岗区二模)已知:BD为△ABC边AC上的高,E为BC上一点,CE=2BE,∠CAE=30°,若EF=3,BF=4,则AF的长为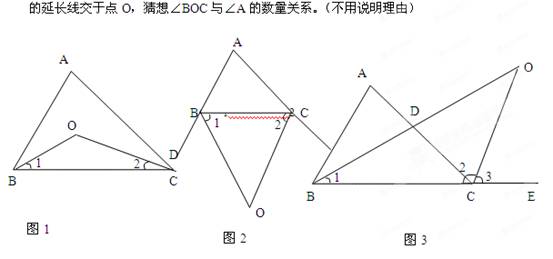 (3)如图3,已知:BD为△ABC的角平分线,CO为△ABC的外角平分线,OB
(3)如图3,已知:BD为△ABC的角平分线,CO为△ABC的外角平分线,OB