题目内容
 如图,∠AOB=∠COD=90°,∠COB=58°,则∠DOA的度数是
如图,∠AOB=∠COD=90°,∠COB=58°,则∠DOA的度数是
- A.112°
- B.122°
- C.142°
- D.102°
B
分析:由于已知∠AOB=∠COD=90°,∠COB=58°,根据图形可以求出∠BOD,∠COA,然后即可求出∠DOA的度数.
解答:∵∠AOB=∠COD=90°,∠COB=58°,
∴∠BOD=∠COA=90°-58°=32°,
∴∠DOA=∠AOB+∠DOB=90°+32°=122°.
故选B.
点评:本题主要考查了垂线的定义和性质,其中也利用了角的和差的关系,解题要注意领会由垂直得直角这一要点.
分析:由于已知∠AOB=∠COD=90°,∠COB=58°,根据图形可以求出∠BOD,∠COA,然后即可求出∠DOA的度数.
解答:∵∠AOB=∠COD=90°,∠COB=58°,
∴∠BOD=∠COA=90°-58°=32°,
∴∠DOA=∠AOB+∠DOB=90°+32°=122°.
故选B.
点评:本题主要考查了垂线的定义和性质,其中也利用了角的和差的关系,解题要注意领会由垂直得直角这一要点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
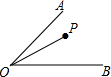 如图,∠AOB=45°,点P为∠AOB内一点,且OP=4,M为OA上一点,N为OB上一点,则△PMN的周长的最小值为( )
如图,∠AOB=45°,点P为∠AOB内一点,且OP=4,M为OA上一点,N为OB上一点,则△PMN的周长的最小值为( )A、4
| ||
B、4
| ||
| C、4 | ||
D、2
|
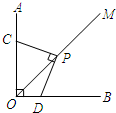 如图,∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C和D,证明:PC=PD.
如图,∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C和D,证明:PC=PD. 如图,∠AOB是一建筑钢架,∠AOB=10°,为使钢架更加稳固,需在内部添加一些钢管EF、FG、GH、HI、IJ,添加钢管的长度都与OE相等,则∠BIJ=( )
如图,∠AOB是一建筑钢架,∠AOB=10°,为使钢架更加稳固,需在内部添加一些钢管EF、FG、GH、HI、IJ,添加钢管的长度都与OE相等,则∠BIJ=( )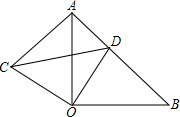 如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.
如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上. 如图,AOB是一条直线,∠AOD=∠COE=90°,则图中∠1的余角是
如图,AOB是一条直线,∠AOD=∠COE=90°,则图中∠1的余角是