Question

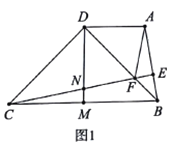
【题目】如图1，四边形中，，，，是边上的中线，过点作垂足为，交线段于点，交于点，连接．

（1）求证：；

（2）探索线段和之间的数量关系，并证明你的结论；

（3）当等于多少度时，点恰好为中点？

Answer 1

【答案】（1）见解析；（2），见解析；（3）105°

【解析】

（1）根据等腰直角三角形的性质得到∠DCB=∠DBC=∠CDM=∠BDM=45°，DM⊥BC，利用ASA定理证明△ABD≌△NCD；

（2）根据全等三角形的性质得到AD=ND，AB=NC，证明△FDA≌△FDN，得到AF=FN，结合图形证明即可；

（3）连接AN，BN，根据线段垂直平分线的性质、等边三角形的判定定理得到△ABN是等边三角形，得到∠BAN=60°，证明△ADN是等腰直角三角形，得到∠DAN=45°，计算即可．

(1) 证明:

(2)

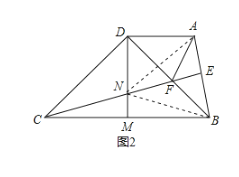
(3)解:如图2，连接AN, BN,

∵CE⊥AB，E为AB中点,

∴直线CE为AB的垂直平分线,

∴AN=BN,

∵AF=FN，AD=DN,

∴直线BD为AN的垂直平分线，

∴AB=NB,

∴AB=AN= BN,

∴△ABN是等边三角形，

∴∠BAN=60°,

∵AD//BC, DM⊥BC,

∴AD⊥DN,

∵AD=DN,

∴△ADN是等腰直角三角形 ,

∴∠DAN=45°,

∴∠BAD=60°+45°=105°．