题目内容
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数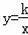
 (x>0,k≠0)的图象经过线段BC的中点D.
(x>0,k≠0)的图象经过线段BC的中点D.
(1)求k的值;
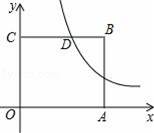
(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.

【考点】反比例函数综合题.
【分析】(1)首先根据题意求出C点的坐标,然后根据中点坐标公式求出D点坐标,由反比例函数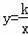
 (x>0,k≠0)的图象经过线段BC的中点D,D点坐标代入解析式求出k即可;
(x>0,k≠0)的图象经过线段BC的中点D,D点坐标代入解析式求出k即可;
(2)分两步进行解答,①当P在直线BC的上方时,即0<x<1,如图1,根据S四边形CQPR=CQ•PD列出S关于x的解析式,②当P在直线BC的下方时,即x>1,如图2,依然根据S四边形CQPR=CQ•PG列出S关于x的解析式.
【解答】解:(1)∵正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),
∴C(0,2),
∵D是BC的中点,
∴D(1,2),
∵反比例函数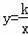
 (x>0,k≠0)的图象经过点D,
(x>0,k≠0)的图象经过点D,
∴k=2;
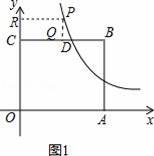
(2)当P在直线BC的上方时,即0<x<1,
如图1,∵点P(x,y)在该反比例函数的图象上运动,
∴y=
 ,
,
∴S四边形CQPR=CQ•PQ=x•(
 ﹣2)=2﹣2x(0<x<1),
﹣2)=2﹣2x(0<x<1),
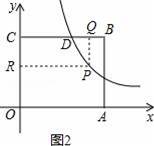
当P在直线BC的下方时,即x>1如图2,同理求出S四边形CQPR=CQ•CR=x•(2﹣
 )=2x﹣2(x>1),
)=2x﹣2(x>1),
综上S=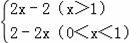
 .
.


【点评】本题主要考查反比例函数的综合题的知识,解答本题的关键是熟练掌握反比例函数的性质,解答(2)问的函数解析式需要分段求,此题难度不大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
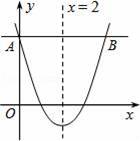
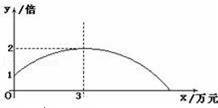
小学生10分钟应用题系列答案某公司销售一种产品,每件产品的成本价、销售价及月销售量如表;为了获取更大的利润,公司决定投入一定的资金做促销广告,结果发现:每月投入的广告费为x万元,产品的月销售量是原销售量的y倍,且y与x的函数图象为如图所示的一段抛物线.
| 成本价(元/件) | 销售价(元/件) | 销售量(万件/月) |
| 2 | 3 | 9 |
(1)求y与x的函数关系式为 ,自变量x的取值范围为 ;
(2)已知利润等于销售总额减去成本费和广告费,要使每月销售利润最大,问公司应投入多少广告费?

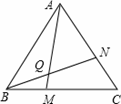 (2)求∠AQN的度数.
(2)求∠AQN的度数.