题目内容
请阅读下面材料:
若![]() ,
,![]() 是抛物线
是抛物线![]() (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线![]() 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
∴  且
且 ![]() ≠
≠![]() .
.
①-②得 ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
又∵ 抛物线![]() (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为![]() ,
,
∴ 直线![]() 为此抛物线的对称轴.
为此抛物线的对称轴.
(1)反之,如果![]() ,
,![]() 是抛物线
是抛物线![]() (a ≠ 0)上不同的
(a ≠ 0)上不同的
两点,直线![]() 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取![]() ,
,![]() 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
(2)利用以上结论解答下面问题:
已知二次函数![]() 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
解:(1)结论:自变量取![]() ,
,![]() 时函数值相等.
时函数值相等.
证明:∵ ![]() ,
,![]() 为抛物线
为抛物线![]() 上不同的两点,
上不同的两点,
|
①-②,得 ![]() .
.
∵ 直线![]() 是抛物线
是抛物线![]() (a ≠ 0)的对称轴,
(a ≠ 0)的对称轴,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() ,即
,即![]()
(阅卷说明:其他代数证明方法相应给分;直接利用抛物线的对称性而
没有用代数方法进行证明的不给分)
(2)∵ 二次函数![]() 当x = 4 时的函数值与x = 2007 时的函数值相等,
当x = 4 时的函数值与x = 2007 时的函数值相等,
∴ 由阅读材料可知二次函数![]() 的对称轴为直线
的对称轴为直线![]() .
.
∴ ![]() ,
,![]() .
.
∴ 二次函数的解析式为![]() .
.
∵ ![]() ,
,
由(1)知,当x = 2012的函数值与![]() 时的函数值相等.
时的函数值相等.
∵ 当x =![]() 时的函数值为
时的函数值为![]() ,
,
∴ 当x = 2012 时的函数值为2011.

若
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.有一种方法证明如下:
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
. ①-②得
 .
.∴
 .
.∴
 .
.又∵ 抛物线
 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
,∴ 直线
 为此抛物线的对称轴.
为此抛物线的对称轴.(1)反之,如果
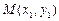 ,
,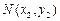 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;(2)利用以上结论解答下面问题:
已知二次函数
 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值. 请阅读下面材料:
若 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
. ①-②得
 .
.∴
 .
.∴
 .
.又∵ 抛物线
 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
,∴ 直线
 为此抛物线的对称轴.
为此抛物线的对称轴.(1)反之,如果
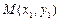 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;(2)利用以上结论解答下面问题:
已知二次函数
 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.  为此抛物线的对称轴.
为此抛物线的对称轴. 且 x1≠x2.
且 x1≠x2.
 ,
, 为此抛物线的对称轴.
为此抛物线的对称轴. 为该抛物线的对称轴,那么自变量取x1,x2时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
为该抛物线的对称轴,那么自变量取x1,x2时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;