题目内容
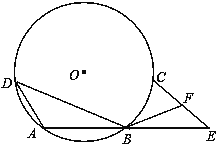
【题目】如图, ![]() 为
为![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,若∠BAC=∠CAM,过点
上一点,若∠BAC=∠CAM,过点![]() 作直线
作直线![]() 垂直于射线AM,垂足为点D.
垂直于射线AM,垂足为点D.
(1)试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,
, ![]() 的半径为3,并且
的半径为3,并且![]() .求
.求![]() 的长.
的长.

【答案】(1)直线CD与⊙O相切,理由见解析(2)CE=![]() .
.
【解析】试题分析:
试题解析:(1)观察图形可得:直线CD与⊙O相切,连接OC.只需要根据条件证明OC⊥CD即可;(2)根据条件可得∠COE=2∠CAB=![]() ,然后在Rt△COE中利用特殊角的三角函数值可求出
,然后在Rt△COE中利用特殊角的三角函数值可求出![]() 的长.
的长.
(1)解:直线CD与⊙O相切. 1分
理由如下:连接OC.

∵OA=OC
∴∠BAC=∠OCA
∵∠BAC=∠CAM
∴∠OCA=∠CAM
∴OC∥AM 5分
∵CD⊥AM
∴OC⊥CD
∴直线![]() 与
与![]() 相切. 7分
相切. 7分
(2)解:
∵![]()
∴∠COE=2∠CAB=![]()
∴在Rt△COE中,OC=3,CE=OC·tan![]() =
=![]() . 10分
. 10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目