题目内容
【题目】如图，矩形ABCD的顶点A，B分别在x轴负半轴，y轴负半轴上，AD交y轴于点F，E为CD的中点．若OB＝1，BD＝2EF时，反比例函数y＝
的图象经过D，E两点，则k的值为_____．
【答案】
【解析】
根据矩形的性质以及勾股定理求出FD＝
＝
＝
BC＝AD，则F为AD中点．如果设A（﹣a，0），a＞0，则B（0，﹣1），D（a，
），C（2a，﹣1），F（0，
），E（
a，﹣）．将E点坐标代入y＝
，求出k＝a，那么F（0，
）．再证明△AOB∽△FOA，得出OA2＝OBOF＝1×＝，求出OA＝
，a＝，进而求出k的值．
解：∵四边形ABCD是矩形，
∴∠ADC＝∠C＝90°，
∵EF＝BD，DE＝CD，
∴FD＝＝＝BC＝AD，
∴F为AD中点；
设A（﹣a，0），a＞0，则B（0，﹣1），D（a，），C（2a，﹣1），F（0，），E（a，﹣）．
∵反比例函数y＝的图象经过E点，
∴a（﹣）＝k，
∴k＝a，
∴F（0，）．
在△AOB与△FOA中，
，
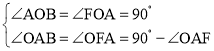∴△AOB∽△FOA，
∴
＝
，
∴OA2＝OBOF＝1×＝，
∴OA＝，
∴a＝，
∴k＝×＝．
故答案为：
．
练习册系列答案
相关题目
