题目内容
 如图,PA、PB分别与⊙O相切于A、B两点,且OP=2,∠APB=60°.若点C在⊙O上,且AC=
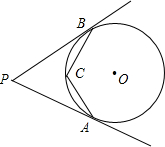
如图,PA、PB分别与⊙O相切于A、B两点,且OP=2,∠APB=60°.若点C在⊙O上,且AC= ,则圆周角∠CAB的度数为________.
,则圆周角∠CAB的度数为________.
15°或75°
分析:首先连接AB,根据题意,可求得∠OAB=30°,OA=1,又由AC= ,由勾股定理的逆定理即可证得△OAC是等腰直角三角形,即可求得∠OAC的度数,继而可求得答案.
,由勾股定理的逆定理即可证得△OAC是等腰直角三角形,即可求得∠OAC的度数,继而可求得答案.
解答: 解:连接AB,
解:连接AB,
∵PA、PB分别与⊙O相切于A、B两点,且∠APB=60°,
∴∠PAO=∠PBO=90°,∠OPA= ∠APB=30°,
∠APB=30°,
∴∠AOB=360°-∠PAO-∠PBO-∠APB=120°,
∵OA=OB,
∴∠OAB=∠OBA= =30°,
=30°,
∵OP=2,
∴OA= OP=1;
OP=1;
∵AB= ,OA=OB=1,
,OA=OB=1,
∴AB2=OA2+OB2,
∴△AOC是直角三角形,
∴∠OAC=45°;
①如图1,若点C在劣弧AB上时,∠CAB=∠OAC-∠OAB=45°-30°=15°;
②如图2,若点C在优弧AB上时,∠CAB=∠OAC+∠OAB=45°+30°=75°.
∴圆周角∠CAB的度数为:15°或75°.
故答案为:15°或75°.
点评:此题考查了切线的性质、圆周角定理以及勾股定理的逆定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与分类讨论思想的应用.
分析:首先连接AB,根据题意,可求得∠OAB=30°,OA=1,又由AC=
 ,由勾股定理的逆定理即可证得△OAC是等腰直角三角形,即可求得∠OAC的度数,继而可求得答案.
,由勾股定理的逆定理即可证得△OAC是等腰直角三角形,即可求得∠OAC的度数,继而可求得答案.解答:
 解:连接AB,
解:连接AB,∵PA、PB分别与⊙O相切于A、B两点,且∠APB=60°,
∴∠PAO=∠PBO=90°,∠OPA=
 ∠APB=30°,
∠APB=30°,∴∠AOB=360°-∠PAO-∠PBO-∠APB=120°,
∵OA=OB,
∴∠OAB=∠OBA=
 =30°,
=30°,∵OP=2,
∴OA=
 OP=1;
OP=1;∵AB=
 ,OA=OB=1,
,OA=OB=1,∴AB2=OA2+OB2,
∴△AOC是直角三角形,
∴∠OAC=45°;
①如图1,若点C在劣弧AB上时,∠CAB=∠OAC-∠OAB=45°-30°=15°;
②如图2,若点C在优弧AB上时,∠CAB=∠OAC+∠OAB=45°+30°=75°.
∴圆周角∠CAB的度数为:15°或75°.
故答案为:15°或75°.
点评:此题考查了切线的性质、圆周角定理以及勾股定理的逆定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
 如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,已知∠P=50°,则∠ACB=
如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,已知∠P=50°,则∠ACB= 7、如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( )
7、如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ) 7、如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是
7、如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是 (2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°.
(2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°. 如图,PA,PB分别切⊙O于点A和点B,C是
如图,PA,PB分别切⊙O于点A和点B,C是