题目内容
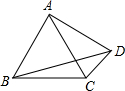
 如图,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则
如图,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则
- A.∠1=∠EFD
- B.BE=EC
- C.BF=DF=CD
- D.FD∥BC
D
分析:根据题中的条件可证明出△ADF≌△ABF,由全等三角形的性质可的∠ADF=∠ABF,再由条件证明出∠ABF=∠C,由角的传递性可得∠ADF=∠C,根据平行线的判定定理可证出FD∥BC.
解答:在△AFD和△AFB中,
∵AF=AF,∠1=∠2,AD=AB,
∴△ADF≌△ABF,
∴∠ADF=∠ABF.
∵AB⊥BC,BE⊥AC,
即:∠BAC+∠C=∠BAC+∠ABF=90°,
∴∠ABF=∠C,
即:∠ADF=∠ABF=∠C,
∴FD∥BC,
故选D.
点评:本题主要考查全等三角形的性质,涉及到的知识点还有平行线的判定定理,关键在于运用全等三角形的性质证明出角与角之间的关系.
分析:根据题中的条件可证明出△ADF≌△ABF,由全等三角形的性质可的∠ADF=∠ABF,再由条件证明出∠ABF=∠C,由角的传递性可得∠ADF=∠C,根据平行线的判定定理可证出FD∥BC.
解答:在△AFD和△AFB中,
∵AF=AF,∠1=∠2,AD=AB,
∴△ADF≌△ABF,
∴∠ADF=∠ABF.
∵AB⊥BC,BE⊥AC,
即:∠BAC+∠C=∠BAC+∠ABF=90°,
∴∠ABF=∠C,
即:∠ADF=∠ABF=∠C,
∴FD∥BC,
故选D.
点评:本题主要考查全等三角形的性质,涉及到的知识点还有平行线的判定定理,关键在于运用全等三角形的性质证明出角与角之间的关系.

练习册系列答案
相关题目
 已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S=
已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S= 12、如图,AB=BC=CD,且∠A=15°,则∠ECD=( )
12、如图,AB=BC=CD,且∠A=15°,则∠ECD=( )
 如图,AB=BC=AC=AD,那么∠BDC等于( )
如图,AB=BC=AC=AD,那么∠BDC等于( ) 如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为
如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为