题目内容
如图,已知直线y= x,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线y=
x,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线y= x上的一点,以点A、B、D为顶点作正方形.
x上的一点,以点A、B、D为顶点作正方形.
(1)若图①仅看作符合条件的一种情况,求出所有符合条件的点D的坐标;
(2)在图①中,若点P以每秒1个单位长度的速度沿直线y= x从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.设点P运动时间为t,试探究:在移动过程中,△PAQ的面积关于t的函数关系式,并求最大值是多少?
x从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.设点P运动时间为t,试探究:在移动过程中,△PAQ的面积关于t的函数关系式,并求最大值是多少?

解:(1)如图,



点D的坐标可以为(7,0)或(16,0)或(28,0);
(2)①当0<t≤3时,如图,过点P作PE⊥x轴,垂足为点E.
AQ=OP=t,OE= t,AE=4-
t,AE=4- t.
t.
S△APQ= AQ•AE=
AQ•AE= t(4-
t(4- t)=
t)= (t-
(t- )2+
)2+

当t= 时,S△APQ的最大值为
时,S△APQ的最大值为 .
.
②当3<t≤5时,如图,
过点P作PE⊥x轴,垂足为点E,过点Q作QF⊥x轴,垂足为点F.
OP=t,PE= t,OE=
t,OE= t,AE=4-
t,AE=4- t.
t.
QF=3,AF=BQ=t-3,EF=AE+AF=1+ t
t
S△APQ=S 梯形PEFQ-S△PEA-S△QFA
 ,由于对称轴为直线
,由于对称轴为直线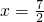 ,故当x=5时,S△APQ的最大值为3.
,故当x=5时,S△APQ的最大值为3.
综上所述,S△APQ的最大值为3.
分析:(1)分情况探讨:点D在x轴上,为正方形的一边或为正方形的对角线;
(2)因为AB之间的距离是 =5,从点O移动到点B的时间最大为5秒,结合Q以相同的速度从点A出发沿着折线A-B-C移动,分两种情况:当点Q与点B重合;点B随着点P的停止而停止;确定t的取值范围,利用面积得出二次函数解决问题.
=5,从点O移动到点B的时间最大为5秒,结合Q以相同的速度从点A出发沿着折线A-B-C移动,分两种情况:当点Q与点B重合;点B随着点P的停止而停止;确定t的取值范围,利用面积得出二次函数解决问题.
点评:此题综合考查了一次函数,二次函数最值问题,并渗透分类讨论思想.



点D的坐标可以为(7,0)或(16,0)或(28,0);
(2)①当0<t≤3时,如图,过点P作PE⊥x轴,垂足为点E.
AQ=OP=t,OE=
 t,AE=4-
t,AE=4- t.
t.S△APQ=
 AQ•AE=
AQ•AE= t(4-
t(4- t)=
t)= (t-
(t- )2+
)2+

当t=
 时,S△APQ的最大值为
时,S△APQ的最大值为 .
.②当3<t≤5时,如图,
过点P作PE⊥x轴,垂足为点E,过点Q作QF⊥x轴,垂足为点F.
OP=t,PE=
 t,OE=
t,OE= t,AE=4-
t,AE=4- t.
t.QF=3,AF=BQ=t-3,EF=AE+AF=1+
 t
tS△APQ=S 梯形PEFQ-S△PEA-S△QFA
 ,由于对称轴为直线
,由于对称轴为直线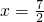 ,故当x=5时,S△APQ的最大值为3.
,故当x=5时,S△APQ的最大值为3.综上所述,S△APQ的最大值为3.
分析:(1)分情况探讨:点D在x轴上,为正方形的一边或为正方形的对角线;
(2)因为AB之间的距离是
 =5,从点O移动到点B的时间最大为5秒,结合Q以相同的速度从点A出发沿着折线A-B-C移动,分两种情况:当点Q与点B重合;点B随着点P的停止而停止;确定t的取值范围,利用面积得出二次函数解决问题.
=5,从点O移动到点B的时间最大为5秒,结合Q以相同的速度从点A出发沿着折线A-B-C移动,分两种情况:当点Q与点B重合;点B随着点P的停止而停止;确定t的取值范围,利用面积得出二次函数解决问题.点评:此题综合考查了一次函数,二次函数最值问题,并渗透分类讨论思想.

练习册系列答案
相关题目
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )