题目内容
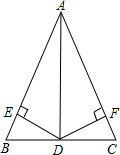 如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.(1)求证:△ABC是等腰三角形.
(2)若∠A=60°,BE=3,求△ABC的周长.
考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:(1)由角平分线的性质可得:DE=DF,然后由HL可证△BED≌△CFD,由全等三角形的对应角相等可得:∠B=∠C,然后由等角对等边可得:AB=AC,即可证:△ABC是等腰三角形.
(2)由△ABC是等腰三角形及∠A=60°,可证△ABC是等边三角形,所以要求△ABC的周长,只需求出BC的长,然后乘以3即可,由∠B=60°,可得∠BDE=30°,然后由直角三角形中30°角所对的直角边等于斜边的一半,可得BD=2BE=6,最后由点D是BC的中点,即可求BC的长度,从而求出△ABC的周长.
(2)由△ABC是等腰三角形及∠A=60°,可证△ABC是等边三角形,所以要求△ABC的周长,只需求出BC的长,然后乘以3即可,由∠B=60°,可得∠BDE=30°,然后由直角三角形中30°角所对的直角边等于斜边的一半,可得BD=2BE=6,最后由点D是BC的中点,即可求BC的长度,从而求出△ABC的周长.
解答:(1)证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC
∴DE=DF,∠BED=∠CFD=90°
∵D是BC的中点
∴BD=CD
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C
∴AB=AC
∴△ABC是等腰三角形
(2)解:∵△ABC是等腰三角形,且∠BAC=60°,
∴△ABC是等边三角形,
∴AB=AC=BC,∠B=∠BAC=∠C=60°,
∴∠BDE=30°,
在Rt△BDE中,∵∠BDE=30°,
∴BD=2BE,
∵BE=3,点D是BC的中点,
∴BC=2BD=4BE=12,
∴△ABC的周长=3BC=36.

∴DE=DF,∠BED=∠CFD=90°
∵D是BC的中点
∴BD=CD
在Rt△BDE和Rt△CDF中,
|
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C
∴AB=AC
∴△ABC是等腰三角形
(2)解:∵△ABC是等腰三角形,且∠BAC=60°,
∴△ABC是等边三角形,
∴AB=AC=BC,∠B=∠BAC=∠C=60°,
∴∠BDE=30°,
在Rt△BDE中,∵∠BDE=30°,
∴BD=2BE,
∵BE=3,点D是BC的中点,
∴BC=2BD=4BE=12,
∴△ABC的周长=3BC=36.
点评:本题主要考查等腰三角形的判定及全等三角形的判定和性质,利用角平分线的性质得出DE=DF是解题的关键.

练习册系列答案
相关题目
若一个多边形的每个外角都为30°,则这个多边形是( )
| A、十二边形 | B、十边形 |
| C、八边形 | D、六边形 |
若(x+2)(x-3)=x2+ax+b,则a,b的值分别为( )
| A、a=5,b=6 |
| B、a=-1,b=6 |
| C、a=5,b=-6 |
| D、a=-1,b=-6 |
P、Q是直线l上的两个不同的点,且OP=5,⊙O的半径为5,下列叙述正确的是( )
| A、点P在⊙O外 |
| B、点Q在⊙O外 |
| C、直线l与⊙O一定相切 |
| D、若OQ=5,则直线l与⊙O相交 |
下列各式中,是最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
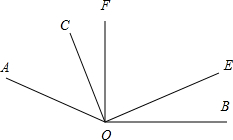 已知∠AOB=160°,∠COE=180°,OF平分∠AOE.如图,若∠COF=14°,则∠BOE=
已知∠AOB=160°,∠COE=180°,OF平分∠AOE.如图,若∠COF=14°,则∠BOE=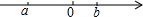 已知数a,b在数轴上表示的点的位置如图所示,则下列结论正确的有( )
已知数a,b在数轴上表示的点的位置如图所示,则下列结论正确的有( )