题目内容
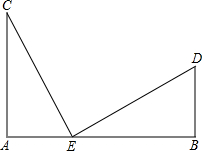 如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD.
如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD.求证:CE=DE,且CE⊥DE.
分析:由AC⊥AB,DB⊥AB可以得出∠CAE=∠EBD=90°,可以得出△AEC≌△BDE,由全等三角形的性质就可以得出结论.
解答:证明:∵AC⊥AB,DB⊥AB,
∴∠CAE=∠EBD=90°.
在△AEC和△BDE中,
,
∴△AEC≌△BDE(SAS),
∴CE=ED,∠C=∠DEB.
∵∠C+∠AEC=90°,
∴∠DEB+∠AEC=90°,
∴∠DEC=90°,
∴CE⊥DE.
∴∠CAE=∠EBD=90°.
在△AEC和△BDE中,
|
∴△AEC≌△BDE(SAS),
∴CE=ED,∠C=∠DEB.
∵∠C+∠AEC=90°,
∴∠DEB+∠AEC=90°,
∴∠DEC=90°,
∴CE⊥DE.
点评:本题考查了垂直的性质及判定的运用,全等三角形的判定与性质的运用,解答本题是得出三角形全等是关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 28、如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
28、如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.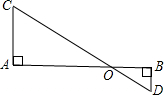 如图,已知AC⊥AB,BD⊥AB,AO=78cm,BO=42cm,CD=159cm,求CO和DO.
如图,已知AC⊥AB,BD⊥AB,AO=78cm,BO=42cm,CD=159cm,求CO和DO. 21、如图,已知AC=AB、AE=AD,∠EAB=∠DAC,求证:BD=CE.
21、如图,已知AC=AB、AE=AD,∠EAB=∠DAC,求证:BD=CE. 如图,已知AC=AB,AE=AD,∠EAB=∠DAC,问BD与EC相等吗?说明理由.
如图,已知AC=AB,AE=AD,∠EAB=∠DAC,问BD与EC相等吗?说明理由.