��Ŀ����
����Ŀ��ʮ��������ʿ��ѧ��ŷ��֤���˼������ж�������![]() ����������
����������![]() ����������
����������![]() ��֮����ڵ�һ����Ȥ�Ĺ�ϵʽ������Ϊŷ����ʽ������۲����м��ּ�����ģ�ͣ�����������⣺
��֮����ڵ�һ����Ȥ�Ĺ�ϵʽ������Ϊŷ����ʽ������۲����м��ּ�����ģ�ͣ�����������⣺
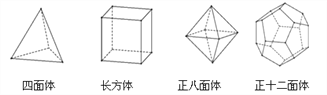
��1���������������ģ�ͣ���ɱ����еĿո�
������ | �������� | ������ | ������ |
������ |
|
| |
������ |
|
|
|
�������� |
|
| |
��ʮ������ |
|
|
|
��1���㷢�ֶ�������![]() ����������
����������![]() ����������
����������![]() ��֮����ڵĹ�ϵʽ��_______.
��֮����ڵĹ�ϵʽ��_______.
��2����ʮ��������![]() �����㣬������______���⣻
�����㣬������______���⣻
��3��һ��������������ȶ�������![]() ������
������![]() ���⣬���������Ķ�������______��
���⣬���������Ķ�������______��
��4��ij��������Ʒ�������Ǽ����壬����������������κͰ˱������ֶ����ƴ�Ӷ��ɣ�����![]() �����㣬ÿ�����㴦����
�����㣬ÿ�����㴦����![]() ���⣬��ö�������������εĸ���Ϊ
���⣬��ö�������������εĸ���Ϊ![]() �����˱��εĸ���Ϊ
�����˱��εĸ���Ϊ![]() ������
������![]() ��ֵ.
��ֵ.
���𰸡��������������1��![]() ����2��30����3��12����4��26.
����2��30����3��12����4��26.
����������1��
������ | �������� | ������ | ������ |
������ |
|
|
|
������ |
|
|
|
�������� |
|
|
|
��ʮ������ |
|
|
|
![]()
��2��![]() ����
����
������![]() ��
��![]()
��3��������������Ϊ![]() ������Ϊ
������Ϊ![]()
![]()
���![]()
��4���⣺����![]() �����㣬
�����㣬![]() ������ȷ��һ���⣬ÿ������
������ȷ��һ���⣬ÿ������![]() ����
����
��![]() ������
������
![]()
���![]()