��Ŀ����
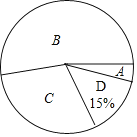
����Ŀ����ͼ1������BPCƽ���ߵķ����ӳ���PA����Ҫ�ֱ��ԡ�APB����APC����BPCΪ�ڽ���������Σ��ұ߳���Ϊ1�����������������������䲻ͬ���ƺ��Ϊһ��ͼ�������磬���ԡ�BPCΪ�ڽǣ�������һ���߳�Ϊ1�������Σ���ʱ��BPC=90������![]() =45��360�����������Ǻͣ���
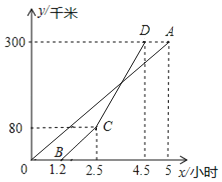
=45��360�����������Ǻͣ���![]() ��������ǡ�ÿ����������߳���Ϊ1�����˱��Σ���仨�ƺ�õ�һ������Ҫ���ͼ������ͼ2��ʾ��
��������ǡ�ÿ����������߳���Ϊ1�����˱��Σ���仨�ƺ�õ�һ������Ҫ���ͼ������ͼ2��ʾ��

ͼ2�е�ͼ���������ܳ���_____��
�����з���Ҫ���ͼ����ѡһ���������ܳ����Ķ�Ϊ��꣬������������ܳ���_____��
���𰸡� 14 21
������������ͼ2����Χ����ӿɵ�ͼ���������ܳ������BPC=2x���ȱ�ʾ�м�������εı��������Ϊ180�㩁2x��������ǺͿɵñ���=![]() ��ͬ���ɵ�����������ε����Ϊx���ɵñ���Ϊ
��ͬ���ɵ�����������ε����Ϊx���ɵñ���Ϊ![]() ���������ܳ��ɵý��ۣ�
���������ܳ��ɵý��ۣ�
ͼ2�е�ͼ���������ܳ��ǣ�8��2+2+8��2=14��
���BPC=2x��
���ԡ�BPCΪ�ڽǵ�������εı���Ϊ��![]() ��
��
�ԡ�APBΪ�ڽǵ�������εı���Ϊ��![]() ��
��
��ͼ���������ܳ���=![]() ��2+
��2+![]() ��2+
��2+![]() ��2=
��2=![]() +
+![]() ��6��
��6��
���������֪��2x��ֵֻ��Ϊ60�㣬90�㣬120�㣬144�㣬
��xԽСʱ���ܳ�Խ��
�൱x=30ʱ���ܳ����ʱͼ����Ϊ��꣬
��������������ܳ���=![]() ��6=21��
��6=21��
�ʴ�Ϊ��14��21��

����Ŀ��ij�н���չ�����߽��й���ѧʷ��Ϊ�����֪ʶ�������������ѧУ�Ա�У100���μ�ѡ������ͬѧ�ijɼ���A��B��C��D�ĸ��ȼ�����ͳ�ƣ����Ƴ����²�������ͳ�Ʊ�������ͳ��ͼ��
�ɼ��ȼ� | Ƶ���������� | Ƶ�� |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
�ϼ� | 100 | 1 |
��1����m=�� ����n=�� ����
��2��������ͳ��ͼ�У�����C�ȼ�������Ӧ�ĽǵĶ�����
��3���ɼ��ȼ�ΪA��4��ͬѧ����1��������3��Ů�����ִ��������ѡ2��ͬѧ����ѧУ�μ�ȫ�б�����������״ͼ�������б������ǡ��ѡ����1��1Ů���ĸ��ʣ�