题目内容
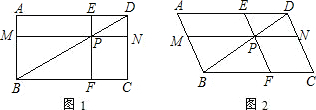
已知四边形ABCD中,P是对角线BD上的一点,过P作MN∥AD,EF∥CD,分别交AB、CD、AD、BC于点M、N、E、F,设a=PM•PE,b=PN•PF,解答下列问题:(1)当四边形ABCD是矩形时,见图1,请判断a与b的大小关系,并说明理由;
(2)当四边形ABCD是平行四边形,且∠A为锐角时,见图2,(1)中的结论是否成立?并说明理由;
(3)在(2)的条件下,设
| BP |
| PD |
| S平行四边形PEAM |
| S△ABD |
| 4 |
| 9 |
分析:(1)当四边形ABCD是矩形时,对角线BD把矩形ABCD分成两个全等三角形,即S△ABD=S△BCD,又MN∥AD,EF∥CD,所以四边形MBFP和四边形PFCN均为矩形,即S△MBF=S△BFP,S△EPD=S△NPD,根据求差法,可知S四边形AMPE=S四边形PFCNA,即a=b;
(2)(1)的方法同时也适用于第二问;
(3)由(1)(2)可知,任意一条过平行四边形对角线交点的直线将把平行四边形分成面积相等的两部分,利用面积之间的关系即可解答.
(2)(1)的方法同时也适用于第二问;
(3)由(1)(2)可知,任意一条过平行四边形对角线交点的直线将把平行四边形分成面积相等的两部分,利用面积之间的关系即可解答.
解答: 解:(1)∵ABCD是矩形,
解:(1)∵ABCD是矩形,
∴MN∥AD,EF∥CD,
∴四边形PEAM、PNCF也均为矩形,
∴a=PM•PE=S矩形PEAM,b=PN•PF=S矩形PNCF,
又∵BD是对角线,
∴△PMB≌△BFP,△PDE≌△DPN,△DBA≌△DBC,
∵S矩形PEAM=S△BDA-S△PMB-S△PDE,
S矩形PNCF=S△DBC-S△BFP-S△DPN,
∴S矩形PEAM=S矩形PNCF,
∴a=b;
(2)成立,理由如下:
∵ABCD是平行四边形,MN∥AD,EF∥CD
∴四边形PEAM、PNCF也均为平行四边形
根据(1)可证S平行四边形PEAM=S平行四边形PNCF,
过E作EH⊥MN于点H,
则sin∠MPE=
EH=PE•sin∠MPE,
∴S?PEAM=PM•EH=PM•PEsin∠MPE,
同理可得S?PNCF=PN•PFsin∠FPN,
又∵∠MPE=∠FPN=∠A,
∴sin∠MPE=sin∠FPN,
∴PM•PE=PN•PF,
即a=b;
(3)方法1:存在,理由如下:
由(2)可知S?PEAM=AE•AMsinA,S?ABCD=AD•ABsinA,
∴
=
=
=
=2•
•
,
又∵
=k,即
=
,
=
,
而
=
=
,
=
=
,
∴2×
×
=
即2k2-5k+2=0,
∴k1=2,k2=
.
故存在实数k=2或
,使得
=
;
方法2:存在,理由如下:
连接AP,设△PMB、△PMA、△PEA、△PED的面积分别为S1、S2、S3、S4,即
=
=
,
=
=
(8分)
即
∴
∴
=
=
即
=
∴2k2-5k+2=0(9分)
∴k1=2,k2=
故存在实数k=2或
,使得
=
.
 解:(1)∵ABCD是矩形,
解:(1)∵ABCD是矩形,∴MN∥AD,EF∥CD,
∴四边形PEAM、PNCF也均为矩形,
∴a=PM•PE=S矩形PEAM,b=PN•PF=S矩形PNCF,
又∵BD是对角线,
∴△PMB≌△BFP,△PDE≌△DPN,△DBA≌△DBC,
∵S矩形PEAM=S△BDA-S△PMB-S△PDE,
S矩形PNCF=S△DBC-S△BFP-S△DPN,
∴S矩形PEAM=S矩形PNCF,
∴a=b;
(2)成立,理由如下:
∵ABCD是平行四边形,MN∥AD,EF∥CD
∴四边形PEAM、PNCF也均为平行四边形
根据(1)可证S平行四边形PEAM=S平行四边形PNCF,
过E作EH⊥MN于点H,
则sin∠MPE=
| EH |
| PE |
∴S?PEAM=PM•EH=PM•PEsin∠MPE,
同理可得S?PNCF=PN•PFsin∠FPN,
又∵∠MPE=∠FPN=∠A,
∴sin∠MPE=sin∠FPN,
∴PM•PE=PN•PF,
即a=b;
(3)方法1:存在,理由如下:
由(2)可知S?PEAM=AE•AMsinA,S?ABCD=AD•ABsinA,
∴
| S平行四边形PEAM |
| S△ABD |
| 2S平行四边形PEAM |
| 2S△ABD |
| 2S平行四边形PEAM |
| S平行四边形ABCD |
| 2AE•AMsinA |
| AD•ABsinA |
| AE |
| AD |
| AM |
| AB |
又∵
| BP |
| PD |
| BP |
| BD |
| k |
| k+1 |
| PD |
| BD |
| 1 |
| k+1 |
而
| AE |
| AD |
| BP |
| BD |
| k |
| k+1 |
| AM |
| AB |
| PD |
| BD |
| 1 |
| k+1 |
∴2×
| k |
| k+1 |
| 1 |
| k+1 |
| 4 |
| 9 |
即2k2-5k+2=0,
∴k1=2,k2=
| 1 |
| 2 |
故存在实数k=2或
| 1 |
| 2 |
| S平行四边形PEAM |
| S△ABD |
| 4 |
| 9 |
方法2:存在,理由如下:
连接AP,设△PMB、△PMA、△PEA、△PED的面积分别为S1、S2、S3、S4,即
| S1 |
| S2 |
| BM |
| AM |
| BP |
| PD |
| S3 |
| S4 |
| AE |
| DE |
| BP |
| PD |
即
|
|
∴
| S平行四边形PEAM |
| S△ABD |
| S2+S3 |
| S1+S2+S3+S4 |
| 4 |
| 9 |
即
| 2kS4 |
| (k2+2k+1)S4 |
| 4 |
| 9 |
∴2k2-5k+2=0(9分)
∴k1=2,k2=
| 1 |
| 2 |
故存在实数k=2或
| 1 |
| 2 |
| S平行四边形PEAM |
| S△ABD |
| 4 |
| 9 |
点评:此题主要考查了平行四边形的性质,在实际中的应用,难易程度适中.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知四边形ABCD中,给出下列四个论断:(1)AB∥CD,(2)AB=CD,(3)AD=BC,(4)AD∥BC.以其中两个论断作为条件,余下两个作为结论,可以构成一些命题.在这些命题中,正确命题的个数有( )
| A、2个 | B、3个 | C、4个 | D、6个 |
选做题:(A)已知四边形ABCD中,AD∥BC,对角线AC、BD交于点O,∠OBC=∠OCB,并且 ,求证:四边形ABCD是 形.(要求在已知条件中的横线上补上一个条件 ,在求证中的横线上添上该四边形的形状,然后画出图形,予以证明,证明时要用上所有条件)
(B)某市市委、市府2001年提出“工业立市”的口号,积极招商引资,财政收入稳步增长,各年度财政收入如下表:
按这种增长趋势,请你算一算2006年该市的财政收入是多少亿元.
(B)某市市委、市府2001年提出“工业立市”的口号,积极招商引资,财政收入稳步增长,各年度财政收入如下表:
| 年 份 | 2001 | 2002 | 2003 | 2004 | … |
| 财政收入 单位(亿元) |
10 | 10.5 | 12 | 14.5 | … |
 如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD=
如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD= 如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,