题目内容
在Rt△ABC中,∠C=90°,c=5,两直角边a、b是关于x的一元二次方程x2-mx+2m-2=0的两个根,则Rt△ABC中较小锐角的正弦值为( ).
A. B.
B. C.
C. D.
D.
C.
【解析】
试题分析:∵a,b是方程x2-mx+2m-2=0的解,
∴a+b=m,ab=2m-2,
在Rt△ABC中,由勾股定理得,a2+b2=c2,
而a2+b2=(a+b)2-2ab,c=5,
∴a2+b2=(a+b)2-2ab=25,
即:m2-2(2m-2)=25
解得,m1=7,m2=-3,
∵a,b是Rt△ABC的两条直角边的长.
∴a+b=m>0,m=-3不合题意,舍去.
∴m=7,
当m=7时,原方程为x2-7x+12=0,
解得,x1=3,x2=4,
不妨设a=3,则sinA= ,
,
∴Rt△ABC中较小锐角的正弦值为 .
.
故选C.
考点:1.锐角三角函数的定义;2.根与系数的关系;3.勾股定理.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为 的小正方形(
的小正方形(
 +ab-2
+ab-2


 ,
, ,则
,则 等于 .
等于 .
 ,求图中阴影部分的面积.(结果保留
,求图中阴影部分的面积.(结果保留 )
) 的一元二次方程的两个根为
的一元二次方程的两个根为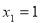 ,
,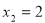 ,则这个方程是( )
,则这个方程是( )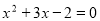 B.
B.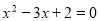
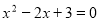 D.
D.
 ,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ABC的外接圆.
,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ABC的外接圆.
 B.
B.
 D.
D.