Question

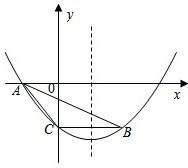如图，抛物线y=a(x-1)2-

4 3

3

经过△ABC的三个顶点，已知点A（-1，0），点C在y轴上，且BC∥x轴．
（1）求a的值；
（2）判断△ABC的形状，并说明理由；
（3）探究：
①若点P是抛物线对称轴上的一个动点，求△PAC周长的最小值；
②若点P是抛物线对称轴且在直线BC上方的一个动点，是否存在点P使△PAB是等腰三角形．若存在，直接写出所有符合条件的点P坐标；不存在，请说明理由．

Answer 1

分析：（1）本题需先把点A的坐标代入抛物线的解析式即可得出a的值；
（2）本题需先根据x=0，得出AC=2，再根据对称性可得点B的坐标，求出BC的值，从而证出AC=BC，即可得出△ABC是等腰三角形；
（3）①本题须先根据题意得出直线AB与对称轴的交点为点P时，△PAC周长的最小，再求出AC+AB的值即可；
②本题需分当PA=AB时，当PB=AB时，当PA=PB时三种情况进行讨论即可得出点P坐标．

解答：解：（1）将点A（-1，0）代入抛物线y=a(x-1)2-

4 3

3

，
得：0=a(-1-1)2-

4 3

3

，
解得a=

3

3

；

（2）△ABC是等腰三角形，
令x=0，则y=

3

3

(0-1)2-

4 3

3

=-

3

，
∴点C（0，-

3

），
∴在Rt△AOC中，AC=

OA2+OC2

=2，
由对称性可得点B（2，-

3

），
∴BC=2，
∴AC=BC，即△ABC是等腰三角形；

（3）①由于点B、C关于抛物线对称轴对称，
所以取直线AB与对称轴的交点为点P时，
△PAC周长的最小，△PAC周长=AC+AB=2+2

3

，
②当PA=AB时，点P坐标为(1，2

2

)，
当PB=AB时，点P坐标为(1，

11

-

3

)，
当PA=PB时，点P坐标为（1，0）．

点评：本题主要考查了二次函数的综合知识，在解题时要能灵活应用二次函数和等腰三角形的有关知识和性质是本题的关键．