题目内容
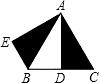△ABC为等边三角形，边长为2cm，D为BC中点，△AEB是△ADC绕点A旋转60°得到的，则∠BAE=________度．
30
分析：根据等边三角形的性质求出∠CAD，再根据旋转变换只改变图形的位置不改变图形的形状与大小可得∠BAE=∠CAD，从而得解．
解答：∵D为等边三角形△ABC的边BC的中点，
∴∠CAD=
×60°=30°，
∵△AEB是△ADC绕点A旋转60°得到，
∴∠BAE=∠CAD=30°．
故答案为：30．
点评：本题考查了旋转的性质，等边三角形的性质，熟记旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键．
分析：根据等边三角形的性质求出∠CAD，再根据旋转变换只改变图形的位置不改变图形的形状与大小可得∠BAE=∠CAD，从而得解．
解答：∵D为等边三角形△ABC的边BC的中点，
∴∠CAD=
×60°=30°，∵△AEB是△ADC绕点A旋转60°得到，
∴∠BAE=∠CAD=30°．
故答案为：30．
点评：本题考查了旋转的性质，等边三角形的性质，熟记旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键．
练习册系列答案
相关题目
16、如图，△ABC为等边三角形，P为三角形内一点，将△ABP绕A点逆时针旋转60°后与△ACP′重合，若AP=3，则PP′=
25、如图，△ABC为等边三角形，D、E为AC和BC边上的两点，且CD=CE，连接ED并延长到F，使AD=DF，连接AF、BD、CF，
25、如图，已知△ABC为等边三角形，CF∥AB，点P为线段AB上任意一点（点P不与A、B重合），过点P作PE∥BC，分别交AC、CF于G、E．
如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD与Q，PQ=4，PE=1．
如图所示，△ABC为等边三角形，BD平分∠ABC，DE⊥BC于E，EC=1，则BC=