题目内容
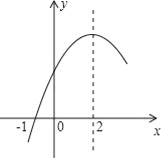
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

【答案】(1)![]() ;(2)45°;(3)
;(2)45°;(3)![]() .
.
【解析】试题分析: ![]() 把点
把点![]() 的坐标代入即可求得抛物线的解析式.
的坐标代入即可求得抛物线的解析式.
![]() 作BH⊥AC于点H,求出
作BH⊥AC于点H,求出![]() 的长度,即可求出∠ACB的度数.
的长度,即可求出∠ACB的度数.
![]() 延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线
延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线![]() 的方程,和抛物线的方程联立即可求得点
的方程,和抛物线的方程联立即可求得点![]() 的坐标.
的坐标.
试题解析:(1)由题意,得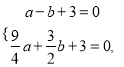
解得![]() .
.
∴这条抛物线的表达式为![]() .
.
(2)作BH⊥AC于点H,
∵A点坐标是(-1,0),C点坐标是(0,3),B点坐标是(![]() ,0),
,0),
∴AC=![]() ,AB=
,AB=![]() ,OC=3,BC=
,OC=3,BC=![]() .
.
∵![]() ,即∠BAD=
,即∠BAD= ![]() ,
,
∴![]() .
.
Rt△ BCH中, ![]() ,BC=
,BC=![]() ,∠BHC=90,
,∠BHC=90,
∴![]() .
.
又∵∠ACB是锐角,∴![]() .
.
(3)延长CD交x轴于点G,
∵Rt△ AOC中,AO=1,AC=![]() ,
,
∴![]() .
.
∵△DCE∽△AOC,∴只可能∠CAO=∠DCE.
∴AG = CG.
∴ .
.
∴AG=5.∴G点坐标是(4,0).
∵点C坐标是(0,3),∴![]() .
.
∴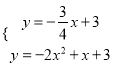 解得
解得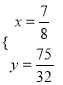 ,
, ![]() (舍).
(舍).
∴点D坐标是![]()

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目