题目内容
(2003•海淀区模拟)已知抛物线y=x2-(a+b)x+ ,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边.
,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边.(1)求证:该抛物线与x轴必有两个不同的交点;
(2)设抛物线与x轴的两个交点为P、Q,顶点为R,且∠PQR=α,tanα=
 ,若△ABC的周长为10,求抛物线的解析式;
,若△ABC的周长为10,求抛物线的解析式;(3)设直线y=ax-bc与抛物线y=x2-(a+b)x+
 交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.
交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.
【答案】分析:(1)抛物线与x轴有两个不同的交点,令y=0,那么得出的方程的△必大于0,已知了a、b、c是三角形的三边,可根据三角形三边关系进行求解.
(2)设抛物线的对称轴与x轴的交点为D,根据α的正切值可得出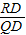 =
=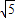 ,根据抛物线的解析式可得出顶点R的坐标,即可得出RD的值,然后根据韦达定理表示出PQ的长,进而可得出QD的表达式,根据α的正切值和a+b+c=10即可求出抛物线的解析式.
,根据抛物线的解析式可得出顶点R的坐标,即可得出RD的值,然后根据韦达定理表示出PQ的长,进而可得出QD的表达式,根据α的正切值和a+b+c=10即可求出抛物线的解析式.
(3)由于△MOE与△MOF等底,因此面积比等于高的比.即两三角形的面积比等于E、F的横坐标的比.可先表示出E、F的横坐标,然后根据横坐标比为5:1求出a、b、c的关系,进而可判断出△ABC的形状.
解答: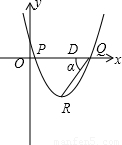 (1)证明:y=x2-(a+b)x+
(1)证明:y=x2-(a+b)x+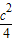
△=(a+b)2-c2=(a+b+c)(a+b-c)(1分)
∵a,b,c为三角形三条边
∴a+b+c>0,a+b>c,a+b-c>0
∴△>0
∴抛物线与x轴必有两个不同交点(2分)
(2)解:设对称轴与x轴交点为D
R(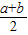 ,
,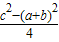 ),
),
∴RD=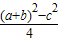
∵PQ=|x1-x2|=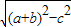 ,DQ=
,DQ=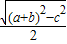 ,tanα=
,tanα=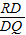 =
=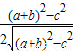 =
=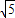
∴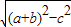 =2
=2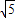 ,
,
∴(a+b)2-c2=20
∵△ABC周长为10,
∴a+b=10-c,(10-c)2-c2=20,c=4,a+b=6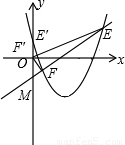
∴y=x2-6x+4
(3)解:y=x2-(a+b)x+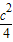
对称轴x=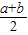 =a,
=a,
∴a=b;
求交点横坐标: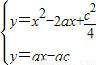
解之得:x2-3ax+ac+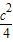 =0
=0
∴x=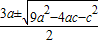
∵抛物线与y轴交点(0,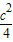 )在y轴正半轴.
)在y轴正半轴.
直线y=ax-bc与y轴交点在y轴负半轴,a>0
∴x1>0,x2>0,
∵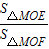 =
=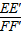 =
=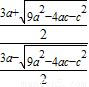 =5
=5
∴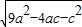 =2a
=2a
∴9a2-4ac-c2=4a2
∴5a2-4ac-c2=0,即(a-c)(5a+c)=0
∵5a+c≠0,
∴a=c
∴a=b=c,△ABC为等边三角形.
点评:本题考查二次函数与一元二次方程的关系、韦达定理、二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.
(2)设抛物线的对称轴与x轴的交点为D,根据α的正切值可得出
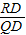 =
=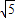 ,根据抛物线的解析式可得出顶点R的坐标,即可得出RD的值,然后根据韦达定理表示出PQ的长,进而可得出QD的表达式,根据α的正切值和a+b+c=10即可求出抛物线的解析式.
,根据抛物线的解析式可得出顶点R的坐标,即可得出RD的值,然后根据韦达定理表示出PQ的长,进而可得出QD的表达式,根据α的正切值和a+b+c=10即可求出抛物线的解析式.(3)由于△MOE与△MOF等底,因此面积比等于高的比.即两三角形的面积比等于E、F的横坐标的比.可先表示出E、F的横坐标,然后根据横坐标比为5:1求出a、b、c的关系,进而可判断出△ABC的形状.
解答:
 (1)证明:y=x2-(a+b)x+
(1)证明:y=x2-(a+b)x+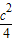
△=(a+b)2-c2=(a+b+c)(a+b-c)(1分)
∵a,b,c为三角形三条边
∴a+b+c>0,a+b>c,a+b-c>0
∴△>0
∴抛物线与x轴必有两个不同交点(2分)
(2)解:设对称轴与x轴交点为D
R(
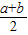 ,
,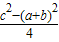 ),
),∴RD=
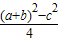
∵PQ=|x1-x2|=
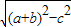 ,DQ=
,DQ=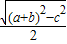 ,tanα=
,tanα=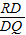 =
=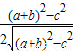 =
=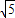
∴
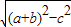 =2
=2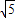 ,
,∴(a+b)2-c2=20
∵△ABC周长为10,
∴a+b=10-c,(10-c)2-c2=20,c=4,a+b=6

∴y=x2-6x+4
(3)解:y=x2-(a+b)x+
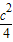
对称轴x=
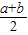 =a,
=a,∴a=b;
求交点横坐标:
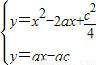
解之得:x2-3ax+ac+
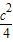 =0
=0∴x=
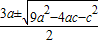
∵抛物线与y轴交点(0,
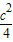 )在y轴正半轴.
)在y轴正半轴.直线y=ax-bc与y轴交点在y轴负半轴,a>0
∴x1>0,x2>0,
∵
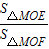 =
=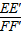 =
=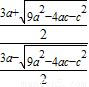 =5
=5∴
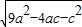 =2a
=2a∴9a2-4ac-c2=4a2
∴5a2-4ac-c2=0,即(a-c)(5a+c)=0
∵5a+c≠0,
∴a=c
∴a=b=c,△ABC为等边三角形.
点评:本题考查二次函数与一元二次方程的关系、韦达定理、二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 )关于y轴对称,如果函数
)关于y轴对称,如果函数 的图象经过点A,那么k= .
的图象经过点A,那么k= .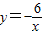 与一次函数y=mx-2的图象都经过点P(a,1),则a、m分别为( )
与一次函数y=mx-2的图象都经过点P(a,1),则a、m分别为( )



 的结果为( )
的结果为( )