题目内容
如图所示，两个同心圆的半径分别为3cm和5cm，弦AB与小圆相切于点C，则AB的长为
- A.8cm
- B.6cm
- C.5cm
- D.4cm
A
分析：作辅助线，连接OC和OB，根据切线的性质圆的切线垂直于过切点的半径，知OC⊥AB，应用勾股定理可将BC的长求出，从而求出AB的长．
解答：解：连接OC和OB，
∵弦AB与小圆相切，
∴OC⊥AB，
在Rt△OBC中，
BC=
=
=4，
∴AB=2BC=8cm．
故选A．
分析：作辅助线，连接OC和OB，根据切线的性质圆的切线垂直于过切点的半径，知OC⊥AB，应用勾股定理可将BC的长求出，从而求出AB的长．
解答：解：连接OC和OB，
∵弦AB与小圆相切，
∴OC⊥AB，
在Rt△OBC中，
BC=
==4，∴AB=2BC=8cm．
故选A．
练习册系列答案
相关题目
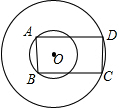如图所示：两个同心圆，半径分别是
（2012•江西模拟）下列几何体中，俯视图是如图所示的两个同心圆的是（ ）
和
，矩形ABCD边AB，CD分别为两圆的弦，当矩形ABCD面积取最大值时，矩形ABCD的周长是 ．
和
，矩形ABCD边AB，CD分别为两圆的弦，当矩形ABCD面积取最大值时，矩形ABCD的周长是 ．