题目内容
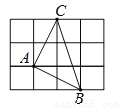
如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A、B、C恰好在网格图中的格点上,那么△ABC中BC边上的高是( )
A. 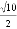 B.
B. 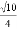 C.
C. 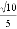 D.
D. 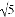
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
题目内容
如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A、B、C恰好在网格图中的格点上,那么△ABC中BC边上的高是( )

A. 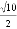 B.
B. 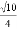 C.
C. 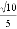 D.
D. 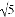
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案