题目内容
阅读下列材料后回答问题:
在平面直角坐标系中,已知x轴上的两点A(X1,0),B(X2,0)的距离记作![]() ,如果
,如果![]() 是平面上任意两点,我们可以通过构造直角三角形来求A、B间的距离。
是平面上任意两点,我们可以通过构造直角三角形来求A、B间的距离。
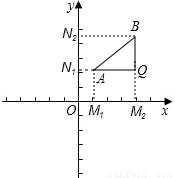
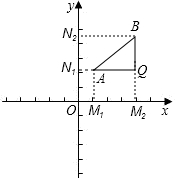
如图,过A、B两点分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别记作![]() ,
,![]() 、
、![]() ,
,![]() ,直线AN1与BM2交于Q点。
,直线AN1与BM2交于Q点。
在Rt△ABQ中,![]() ,∵
,∵![]() ,
,![]()
∴![]()
由此得任意两点![]() 之间的距离公式:
之间的距离公式:![]()
如果某圆的圆心为(0,0),半径为r。设P(x,y)是圆上任一点,根据“圆上任一点到定点(圆心)的距离都等于定长(半径)”,我们不难得到![]() ,即:
,即:![]() , 整理得:
, 整理得:![]() 。我们称此式为圆心在原点,半径为r的圆的方程。
。我们称此式为圆心在原点,半径为r的圆的方程。
(1)直接应用平面内两点间距离公式,求点![]() 之间的距离;
之间的距离;
(2)如果圆心在点P(2,3),半径为3,求此圆的方程。
(3)方程![]() 是否是圆的方程?如果是,求出圆心坐标与半径。
是否是圆的方程?如果是,求出圆心坐标与半径。
解(1):利用![]()
把![]() 代入上式
代入上式
![]()
(2)![]()
(3)∵方程![]() 可以变形为
可以变形为![]() ,
,
所以它是圆的方程,圆心坐标为(6,-4),半径为4。

练习册系列答案
相关题目
 原点,半径为r的圆的方程.
原点,半径为r的圆的方程.
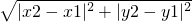
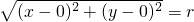 ,整理得:x2+y2=r2.我们称此式为圆心在
,整理得:x2+y2=r2.我们称此式为圆心在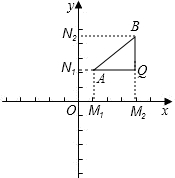 原点,半径为r的圆的方程.
原点,半径为r的圆的方程.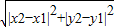
 ,整理得:x2+y2=r2.我们称此式为圆心在原点,半径为r的圆的方程.
,整理得:x2+y2=r2.我们称此式为圆心在原点,半径为r的圆的方程.