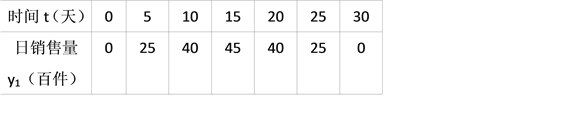��Ŀ����
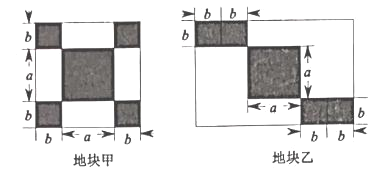
����Ŀ�����Ķ����ϣ���ͼ(1),�������ϵ�![]() ʾ����Ϊ
ʾ����Ϊ![]() ���ʾ����Ϊ
���ʾ����Ϊ![]() ,���
,���![]() ����
����![]() �ľ����Ϊ
�ľ����Ϊ![]() ,�߶�
,�߶�![]() �ij��������ұߵ�����ȥ��ߵ�����ʾ,��
�ij��������ұߵ�����ȥ��ߵ�����ʾ,��![]()
![]()
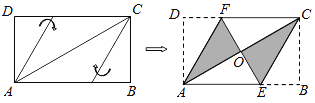
������⣺��ͼ(2),�����ϵ�![]() ��ʾ������
��ʾ������![]() ,��
,��![]() ��ʾ������
��ʾ������![]() ,����
,����![]() ����
����![]() ��ʾ������
��ʾ������![]() ��
��
![]()
(1)����������һ��![]() ,��
,��![]() ,���
,���![]() ��ʾ����Ϊ______.
��ʾ����Ϊ______.
(2)����![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ������˶���
����λ���ȵ��ٶ������˶���![]() ,ͬʱ��
,ͬʱ��![]() �͵�
�͵�![]() �ֱ���ÿ��
�ֱ���ÿ��![]() ����λ���Ⱥ�
����λ���Ⱥ�![]() ����λ���ȵ��ٶ������˶��ֱ�
����λ���ȵ��ٶ������˶��ֱ�![]() ,����
,����![]() ���ӹ���,����
���ӹ���,����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ,��
,��![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ,��
,��![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() �����
�����![]() ��ʾ������______,
��ʾ������______,![]() =________
=________![]() �ú�
�ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() ��
��
(3)���ʣ�![]() ��ֵ�Ƿ�����ʱ��
��ֵ�Ƿ�����ʱ��![]() �ı仯���ı䣿���仯,��˵�����ɣ�������,������ֵ.
�ı仯���ı䣿���仯,��˵�����ɣ�������,������ֵ.
(4)����![]() ��
��![]() �ֱ���
�ֱ���![]() ����λÿ���
����λÿ���![]() ����λÿ����ٶ�������У������A��C�������
����λÿ����ٶ�������У������A��C�������![]() ����λ���ȣ�
����λ���ȣ�
���𰸡�(1)-7��-1��(2)-4-![]() t��4+t��(3)���䣬��ֵΪ4��(4)t=2��t=
t��4+t��(3)���䣬��ֵΪ4��(4)t=2��t=![]() .
.
��������
��1�����ݷǸ������������a��b��ֵ�����ɾ���Ķ�����⼴�ɣ�
��2�����������ʾ����![]() ��
��![]() ��
��![]() ����ʾ���������ɵó����ۣ�
����ʾ���������ɵó����ۣ�
��3�������![]() ��Ȼ����뻯�ɵó����ۣ�
��Ȼ����뻯�ɵó����ۣ�
��4�������A��·��Ϊ4t����C��·��Ϊ2t��Ȼ���Ϊ����ǰ���![]() ����λ���Ⱥ����������
����λ���Ⱥ����������![]() ����λ�����з��̣���⼴�ɣ�
����λ�����з��̣���⼴�ɣ�
��1���ɷǸ��������ʿɵõ���a+4=0��b��2=0����ã�a=��4��b=2��
��D��ʾ����Ϊx����AD=x������4��=3��4��x=3����ã�x=��1��x=��7��
�ʴ�Ϊ����7��1��
��2���������֪����![]() ��ʾ�����ǣ�
��ʾ�����ǣ�![]() ����
����![]() ��ʾ�����ǣ�
��ʾ�����ǣ�![]() ����
����![]() ��ʾ�����ǣ�
��ʾ�����ǣ�![]() ����
����![]() =
=![]() ����
����![]() ��=
��=![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3���ɣ�2���ã�![]() =
= ![]() ����
����![]() ��=
��=![]() =
=![]() ����
����![]() =
=![]() =
=![]() =4����
=4����![]() Ϊ��ֵ4��
Ϊ��ֵ4��
��4��������ã���A��·��Ϊ4t����C��·��Ϊ2t����4t+2t=10+2��4t+2t=10��2����ã�t=2��t=![]() ��
��

 â���̸������Ծ�ϵ�д�
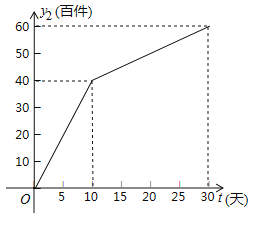
â���̸������Ծ�ϵ�д�����Ŀ�������̳���Ӫij��Ʒ�Ƶ�T��������ʱ�ĵ�����300Ԫ�������г����飺��һ��ʱ���ڣ����۵�����400Ԫʱ����������60�������۵���ÿ��10Ԫ���������ͼ���1����������T�������۵���ΪxԪ��x��400��ʱ��������Ϊy������������ΪWԪ��
��1����ֱ��ú�x�Ĵ���ʽ��ʾy��W���ѽ�������±�����
���۵��ۣ�Ԫ�� | x |
������y������ | |
��������W��Ԫ�� |
��2�����̳��ƻ�ʵ����������10000Ԫ������������������������ôx��ֵӦ���Ƕ��٣�