题目内容
24、（1）用量角器画△ABC的角平分线BE、CF相交于P，（2）如果∠ABC=70°，∠ACB=60°，则∠BPC=
115
°．分析：（1）分别量出∠B，∠C的度数，进而作出三角形的角平分线BE、CF，交于P；
（2）利用角平分线的性质和三角形的内角和定理可得所求角的度数．
（2）利用角平分线的性质和三角形的内角和定理可得所求角的度数．
解答：解：（1）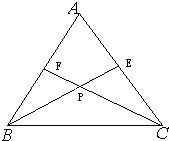
；
（2）∵∠ABC=70°，∠ACB=60°，BE，CF是三角形的角平分线，
∴∠PBC=35°，∠PCB=30°，
∴∠BPC=180°-∠PBC-∠PCB=115°．
故答案为115．
；（2）∵∠ABC=70°，∠ACB=60°，BE，CF是三角形的角平分线，
∴∠PBC=35°，∠PCB=30°，
∴∠BPC=180°-∠PBC-∠PCB=115°．
故答案为115．
点评：综合考查了三角形内角和定理和角平分线的性质；得到所求角的关系式是解决本题的关键．
练习册系列答案
相关题目
