Question

（1）解方程：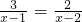
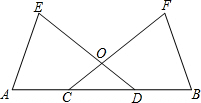
（2）如图，在等腰梯形ABFE中，点C、D 在线段AB上，连接DE、CF．DE与CF相交于点O，且AC=BD，求证：DE=CF．

Answer 1

（1）解：方程两边同时乘以（x-1）（x-2）得：
3（x-2）=2（x-1），
即3x-6=2x-2，
解得：x=4，
经检验：当x=4时，（x-1）（x-2）=（4-1）（4-2）=6≠0
∴x=4是方程的解；

（2）证明：∵AC=BD，
∴AD=BC，
∵ABFE是等腰梯形，
∴∠A=∠B，
又∵AE=BF，
∴△ADE≌△BCF，
∴DE=CF．
分析：（1）方程两边同时乘以（x-1）（x-2），即可转化为一个一元一次方程，从而求解；
（2）要证明DE=CF，可以转化为证明△ADE≌△BCF，根据SAS即可证明．
点评：本题主要考查了分式方程的解法以及等腰梯形的性质，解分式方程的基本思想是通过去分母转化为整式方程，证明线段相等一般可以转化为证明三角形全等．