Question

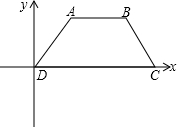如图，等腰梯形ABCD中，∠ADC=60°，AB=2，CD=6，则各顶点的坐标是A（2，2

3

），B

 

，C

 

，D（0，0）．

Answer 1

分析：作AE⊥x轴，BF⊥x轴分别于E，F，根据等腰梯形的性质，分别求出DE、FC、DF的长，然后根据点A的坐标和点D的坐标求出BF的长，即可解答此题．

解答：解：作AE⊥x轴，BF⊥x轴分别于E，F．
则DE=FC=

6-2

2

=2，
∴DF=2+2=4，
由点A的坐标（2，2

3

）和点D的坐标（0，0），
得出BF=2

3

，
∴B点的坐标是B（4，2

3

）；C（6，0）．
故答案分别为：（4，2

3

）；（6，0）．

点评：此题主要考查学生对等腰梯形的性质、坐标与图形性质的理解和掌握，此类等腰梯形的问题可以通过作高线转化为直角三角形或矩形的问题，求点的坐标的问题转化为求线段的长的问题．