题目内容
如图，直线AB、CD相交于点O，OE⊥CD，∠BOE=54°，则∠AOC等于
- A.54°
- B.46°
- C.36°
- D.26°
C
分析：根据余角的定义、对顶角相等推知∠AOC=∠BOD=90°-∠BOE．
解答：如图，∵OE⊥CD，
∴∠DOE=90°．
又∵∠BOE=54°，
∴∠BOD=90°-∠BOE=36°，
∴∠AOC=∠BOD=36°．
故选C．
点评：本题考查了垂线，对顶角、邻补角．解题时，注意挖掘出隐含在题中的已知条件：由垂直得直角．
分析：根据余角的定义、对顶角相等推知∠AOC=∠BOD=90°-∠BOE．
解答：如图，∵OE⊥CD，
∴∠DOE=90°．
又∵∠BOE=54°，
∴∠BOD=90°-∠BOE=36°，
∴∠AOC=∠BOD=36°．
故选C．
点评：本题考查了垂线，对顶角、邻补角．解题时，注意挖掘出隐含在题中的已知条件：由垂直得直角．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
21、如图，直线AB、CD、EF都经过点O，且AB⊥CD，∠COE=35°，求∠DOF、∠BOF的度数．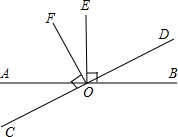
如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD．
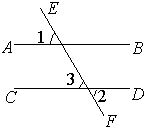25、完成推理填空：如图：直线AB、CD被EF所截，若已知AB∥CD，
如图，直线AB、CD、EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD=24°，∠COG的度数=
如图，直线AB，CD相交于O点，EO⊥CD，垂足为O点，若∠BOE=50°，求∠AOD的度数．