ĢāÄæÄŚČŻ
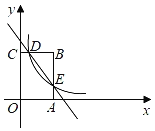
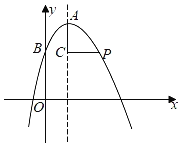
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖÅ×ĪļĻߵĶ„µćĪŖA(2£¬![]() )£¬Å×ĻßĪļÓėyÖį½»ÓŚµćB(0£¬
)£¬Å×ĻßĪļÓėyÖį½»ÓŚµćB(0£¬![]() )£¬µćCŌŚĘä¶Ō³ĘÖįÉĻĒŅĪ»ÓŚµćAĻĀ·½£¬½«Ļ߶ĪACČʵćC°“Ė³Ź±Õė·½ĻņŠż×Ŗ90”ć£¬µćAĀäŌŚÅ×ĪļĻßÉĻµÄµćP“¦£®
)£¬µćCŌŚĘä¶Ō³ĘÖįÉĻĒŅĪ»ÓŚµćAĻĀ·½£¬½«Ļ߶ĪACČʵćC°“Ė³Ź±Õė·½ĻņŠż×Ŗ90”ć£¬µćAĀäŌŚÅ×ĪļĻßÉĻµÄµćP“¦£®
(1)ĒóÅ×ĪļĻߵĽāĪöŹ½£»
(2)ĒóĻ߶ĪACµÄ³¤£»
(3)½«Å×ĪļĻßĘ½ŅĘ£¬Ź¹Ę䶄µćAŅʵ½ŌµćOµÄĪ»ÖĆ£¬ÕāŹ±µćPĀäŌŚµćDµÄĪ»ÖĆ£¬Čē¹ūµćMŌŚyÖįÉĻ£¬ĒŅŅŌO£¬C£¬D£¬MĪŖ¶„µćµÄĖıߊĪµÄĆ껿ĪŖ8£¬ĒóµćMµÄ×ų±ź£®
”¾“š°ø”æ(1)y£½©![]() (x©2)2+
(x©2)2+![]() £»(2)2£»(3)MµćµÄ×ų±źĪŖ(0£¬
£»(2)2£»(3)MµćµÄ×ų±źĪŖ(0£¬![]() )»ņ(0£¬©
)»ņ(0£¬©![]() )
)
”¾½āĪö”æ
£Ø1£©ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖ£ŗy=a£Øx-2£©2+![]() £¬½«µćB×ų±ź“śČėæÉĒóaµÄÖµ£¬¼“æÉĒó½ā£»
£¬½«µćB×ų±ź“śČėæÉĒóaµÄÖµ£¬¼“æÉĒó½ā£»
£Ø2£©ÉčAC=t£¬ŌņµćC£Ø2£¬![]() -t£©£¬ĄūÓĆ²ĪŹżt±ķŹ¾µćP×ų±ź£¬“śČė½āĪöŹ½æÉĒó½ā£»
-t£©£¬ĄūÓĆ²ĪŹżt±ķŹ¾µćP×ų±ź£¬“śČė½āĪöŹ½æÉĒó½ā£»
£Ø3£©ÓÉĘ½ŅʵĊŌÖŹæÉĒóµćD×ų±ź£¬ÓÉĆ껿¹«Ź½æÉĒó½ā£®
½ā£ŗ(1)ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖ£ŗy£½a(x©2)2+![]() £¬
£¬
”ßÅ×ĻßĪļÓėyÖį½»ÓŚµćB(0£¬![]() )£¬
)£¬
”ą![]() £½a(0©2)2+
£½a(0©2)2+![]() £¬
£¬
”ąa£½©![]()
”ąĪļĻߵĽāĪöŹ½ĪŖ£ŗy£½©![]() (x©2)2+
(x©2)2+![]() £»
£»
(2)”߶„µćA(2£¬![]() )£¬
)£¬
”ąÅ×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx£½2£¬
”ąÉčAC£½t£¬ŌņµćC(2£¬![]() ©t)£¬
©t)£¬
”ß½«Ļ߶ĪACČʵćC°“Ė³Ź±Õė·½ĻņŠż×Ŗ90”ć£¬µćAĀäŌŚÅ×ĪļĻßÉĻµÄµćP“¦£®
”ą”ĻACP£½90”ć£¬AC£½PC£½t£¬
”ąµćP(2+t£¬![]() ©t)£¬
©t)£¬
”ßµćPŌŚÅ×ĪļĻßÉĻ£¬
”ą![]() ©t£½©
©t£½©![]() (2+t©2)2+
(2+t©2)2+![]() £¬
£¬
”ąt1£½0(²»ŗĻĢāŅāÉįČ„)£¬t2£½2£¬
”ąĻ߶ĪACµÄ³¤ĪŖ2£»
(3)”ßAC£½2£¬Pµć×ų±źĪŖ(4£¬![]() )£¬Cµć×ų±źĪŖ(2£¬
)£¬Cµć×ų±źĪŖ(2£¬![]() )£¬
)£¬
”ßÅ×ĪļĻßĘ½ŅĘ£¬Ź¹Ę䶄µćA(2£¬![]() )Ņʵ½ŌµćOµÄĪ»ÖĆ£¬
)Ņʵ½ŌµćOµÄĪ»ÖĆ£¬
”ąÅ×ĪļĻßĻņ×óĘ½ŅĘ2øöµ„Ī»£¬ĻņĻĀĘ½ŅĘ![]() øöµ„Ī»£¬
øöµ„Ī»£¬
¶ųPµć(4£¬![]() )Ļņ×óĘ½ŅĘ2øöµ„Ī»£¬ĻņĻĀĘ½ŅĘ
)Ļņ×óĘ½ŅĘ2øöµ„Ī»£¬ĻņĻĀĘ½ŅĘ![]() øöµ„Ī»µĆµ½µćD£¬
øöµ„Ī»µĆµ½µćD£¬
”ąDµć×ų±źĪŖ(2£¬©2)£¬
ÉčM(0£¬m)£¬
µ±m£¾0Ź±£¬![]() (m+
(m+![]() +2)2£½8£¬½āµĆm£½
+2)2£½8£¬½āµĆm£½![]() £¬“ĖŹ±Mµć×ų±źĪŖ(0£¬
£¬“ĖŹ±Mµć×ų±źĪŖ(0£¬![]() )£»
)£»
µ±m£¼0Ź±£¬![]() (©m+
(©m+![]() +2)2£½8£¬½āµĆm£½©
+2)2£½8£¬½āµĆm£½©![]() £¬“ĖŹ±Mµć×ų±źĪŖ(0£¬©
£¬“ĖŹ±Mµć×ų±źĪŖ(0£¬©![]() )£»
)£»
×ŪÉĻĖłŹö£¬MµćµÄ×ų±źĪŖ(0£¬![]() )»ņ(0£¬©
)»ņ(0£¬©![]() )£®
)£®

”¾ĢāÄæ”æĪŖĮĖ½āijŠ£³õ¶žŃ§ÉśĆæÖÜÉĻĶųµÄŹ±¼ä£¬Į½Ī»Ń§Éś½ųŠŠĮĖ³éŃłµ÷²é£®Š”Ąöµ÷²éĮĖ³õ¶žµēÄŌ°®ŗĆÕßÖŠ40ĆūѧɜĆæÖÜÉĻĶųµÄŹ±¼ä£»Š”½Ü“ÓČ«Š£400Ćū³õ¶žŃ§ÉśÖŠĖ껜³éČ”ĮĖ40Ćūѧɜ£¬µ÷²éĮĖĆæÖÜÉĻĶųµÄŹ±¼ä£®Š”ĄöÓėŠ”½ÜÕūĄķø÷×ŌŃł±¾Źż¾Ż£¬ČēĻĀ±ķĖłŹ¾£ŗ
Ź±¼ä¶Ī £ØŠ”Ź±£ÆÖÜ£© | Š”Ąö³éŃł ČĖŹż | Š”½Ü³éŃł ČĖŹż |
0”«1 | 6 | 22 |
1”«2 | 10 | 10 |
2”«3 | 16 | 6 |
3”«4 | 8 | 2 |
£ØĆæ×éæÉŗ¬×īµĶÖµ£¬²»ŗ¬×īøßÖµ£©
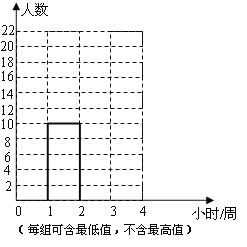
£Ø1£©ÄćČĻĪŖÄÄĪ»Ķ¬Ń§³éČ”µÄŃł±¾²»ŗĻĄķ£æĒėĖµĆ÷ĄķÓÉ£»
£Ø2£©øł¾ŻŗĻĄķ³éČ”µÄŃł±¾£¬°ŃÉĻĶ¼ÖŠµÄʵŹż·Ö²¼Ö±·½Ķ¼²¹»ĶźÕū£»
£Ø3£©×ؼŅ½ØŅéĆæÖÜÉĻĶų2Š”Ź±ŅŌÉĻ£Øŗ¬2Š”Ź±£©µÄĶ¬Ń§Ó¦ŹŹµ±¼õÉŁÉĻĶųµÄŹ±¼ä£¬¹Ą¼ĘøĆŠ£Č«Ģå³õ¶žŃ§ÉśÖŠÓŠ¶ąÉŁĆūĶ¬Ń§Ó¦ŹŹµ±¼õÉŁÉĻĶųµÄŹ±¼ä£æ