题目内容
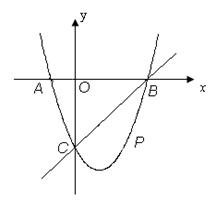
(本题12分) 如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求b,c的值.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形![]() ,那么是否存在点P,使四边形
,那么是否存在点P,使四边形 为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
 (3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
解:(1)将B、C两点的坐标代入得![]() …………2分
…………2分
解得:![]()
所以二次函数的表达式为:![]() …………3分
…………3分
 (2)存在点P,使四边形
(2)存在点P,使四边形![]() 为菱形.设P点坐标为(x,
为菱形.设P点坐标为(x,![]() ),
),![]() 交CO于E
交CO于E
若四边形![]() 是菱形,则有PC=PO.连结
是菱形,则有PC=PO.连结![]() , 则PE⊥CO于E,∴OE=EC=
, 则PE⊥CO于E,∴OE=EC=![]() ∴
∴![]() =
=![]() . ………5分
. ………5分
∴![]() =
=![]()
解得![]() =
=![]() ,
,![]() =
=![]() (不合题意,舍去)
(不合题意,舍去)
∴P点的坐标为(![]() ,
,![]() ) ………………7分
) ………………7分
(3)过点P作![]() 轴的平行线与BC交于点Q,与OB交于点F,
轴的平行线与BC交于点Q,与OB交于点F,
设P(x,![]() ),
),
易得,直线BC的解析式为![]()
则Q点的坐标为(x,x-3).

![]()
![]()
=![]() …………10分
…………10分
当![]() 时,四边形ABPC的面积最大
时,四边形ABPC的面积最大
此时P点的坐标为![]() ,四边形ABPC的面积
,四边形ABPC的面积![]() . …………12分
. …………12分
解析:略

练习册系列答案
相关题目




 x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y=