题目内容
 28、如图,点A的坐标为(4,5),点B的坐标为(-6,-1),分别在x轴和y轴上找一点C和D,使得以A、B、C、D为顶点的四边形是平行四边形,求出点C和点D的坐标.
28、如图,点A的坐标为(4,5),点B的坐标为(-6,-1),分别在x轴和y轴上找一点C和D,使得以A、B、C、D为顶点的四边形是平行四边形,求出点C和点D的坐标.分析:分类讨论,(1)当AB为平行四边形的一条边时,①点C在x轴的正半轴,②点C在x轴的负半轴时,(2)当AB是对角线时,分别设出点C和点D的坐标求解即可.
解答:解:当AB是平行四边形一条边,且点C在x轴的正半轴时,AD与BC互相平分,设点C的坐标为(a,0),点D的坐标为(0,b),
由上面的结论可知:-6+a=4+0,-1+0=5+b,
∴a=10,b=-6,
∴此时点C的坐标为(10,0),点D的坐标为(0,-6),
同理,当AB是平行四边形一条边,且点C在x轴的负半轴时,
求得点C的坐标为(-10,0),点D的坐标为(0,6),
当AB是对角线时,点C的坐标为(-2,0),点D的坐标为(0,4).
由上面的结论可知:-6+a=4+0,-1+0=5+b,
∴a=10,b=-6,
∴此时点C的坐标为(10,0),点D的坐标为(0,-6),
同理,当AB是平行四边形一条边,且点C在x轴的负半轴时,
求得点C的坐标为(-10,0),点D的坐标为(0,6),
当AB是对角线时,点C的坐标为(-2,0),点D的坐标为(0,4).
点评:本题考查了平行四边形的性质,分类讨论是本题的关键,当AB是边时还要分两种情况,同学们要注意思考,避免漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 如图,点A的坐标为( )
如图,点A的坐标为( )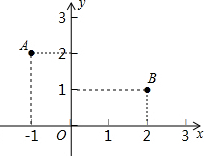 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )