题目内容
已知:直角梯形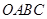 中,
中,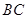 ∥
∥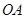 ,∠
,∠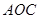 =
=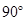 ,以
,以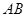 为直径的圆
为直径的圆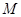 交
交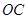 于点
于点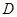 、
、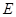 ,连结
,连结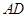 、
、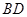 、
、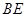 .
.
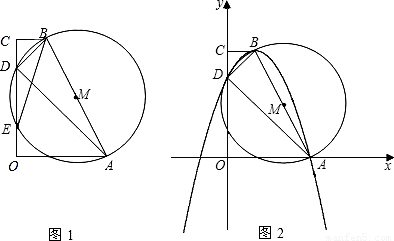
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形:
_____________________,______________________ ;
(2)直角梯形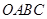 中,以
中,以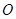 为坐标原点,
为坐标原点,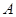 在
在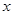 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线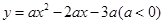 经过点
经过点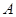 、
、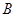 、
、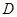 ,且
,且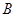 为抛物线的顶点.
为抛物线的顶点.
①写出顶点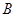 的坐标(用含
的坐标(用含 的代数式表示)___________;
的代数式表示)___________;
②求抛物线的解析式;
③在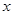 轴下方的抛物线上是否存在这样的点
轴下方的抛物线上是否存在这样的点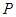 ,过点
,过点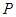 作
作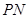 ⊥
⊥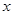 轴于点
轴于点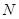 ,使得以点
,使得以点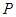 、
、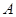 、
、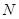 为顶点的三角形与△
为顶点的三角形与△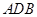 相似?若存在,求出点
相似?若存在,求出点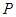 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】
(1)△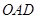 ∽△
∽△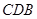 ,△
,△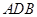 ∽△
∽△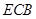 .……………4分
.……………4分
(2)①(1,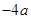 )…………………………………………1分
)…………………………………………1分
②抛物线的解析式为: ………………3分
………………3分
③当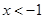 时,点
时,点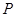 为(
为(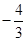 ,
,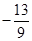 )、(
)、(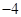 ,
,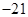 )………………2分
)………………2分
当 时,两个点
时,两个点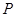 不存在 …………………………………2分
不存在 …………………………………2分
【解析】(1)由圆周角定理知:∠ADB=90°,首先可联想到的相似三角形是△BCD和△DOA;易知∠BAD=∠BED,可得的另一对相似三角形是Rt△ABD和Rt△EBC;
(2)①用公式法或配方法均能求出顶点B的坐标;
②根据抛物线的解析式,易求得B、D、A的坐标,也就得到了OA、OD、CD、BC的长,根据(1)得出的相似三角形,即可根据对应的成比例线段求出a的值,也就能求出抛物线的解析式;
③由②易知△OAD是等腰Rt△,若△PAN与△OAD相似,则△PAN也必须是等腰Rt△;可根据抛物线的解析式设出P点坐标,然后根据PN=AN的条件来求出P点的坐标

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 中,
中,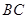 ∥
∥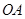 ,∠
,∠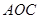 =
=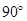 ,以
,以 为直径的圆
为直径的圆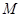 交
交 于点
于点 、
、 ,连结
,连结 、
、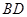 、
、 .
.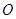 为坐标原点,
为坐标原点, 在
在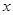 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线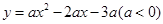 经过点
经过点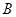 、
、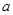 的代数式表示)___________;
的代数式表示)___________;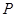 ,过点
,过点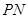 ⊥
⊥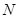 ,使得以点
,使得以点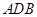 相似?若存在,求出点
相似?若存在,求出点
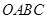 中,
中,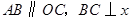 轴于点
轴于点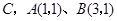 .动点
.动点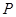 从
从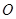 点出发,沿
点出发,沿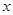 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过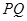 垂直于直线
垂直于直线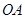 ,垂足为
,垂足为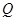 .设
.设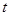 秒(
秒(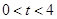 ),
),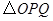 与直角梯形
与直角梯形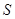 .
.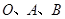 三点的抛物线解析式;
三点的抛物线解析式;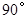 ,是否存在
,是否存在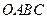 中,
中,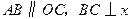 轴于点
轴于点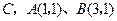 .动点
.动点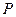 从
从 点出发,沿
点出发,沿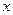 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过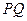 垂直于直线
垂直于直线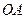 ,垂足为
,垂足为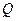 .设
.设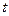 秒(
秒(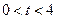 ),
),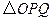 与直角梯形
与直角梯形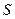 .
.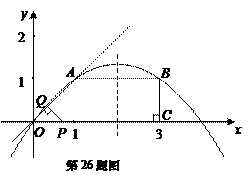
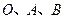 三点的抛物线解析式;
三点的抛物线解析式;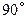 ,是否存在
,是否存在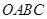 中,
中,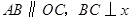 轴于点
轴于点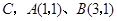 .动点
.动点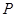 从
从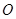 点出发,沿
点出发,沿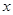 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过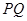 垂直于直线
垂直于直线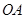 ,垂足为
,垂足为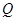 .设
.设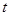 秒(
秒(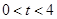 ),
),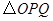 与直角梯形
与直角梯形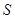 .
.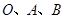 三点的抛物线解析式;
三点的抛物线解析式; ,是否存在
,是否存在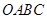 中,
中,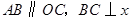 轴于点
轴于点 .动点
.动点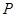 从
从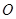 点出发,沿
点出发,沿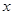 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过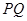 垂直于直线
垂直于直线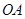 ,垂足为
,垂足为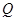 .设
.设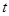 秒(
秒(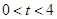 ),
),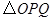 与直角梯形
与直角梯形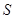 .
.
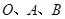 三点的抛物线解析式;
三点的抛物线解析式; ,是否存在
,是否存在