题目内容
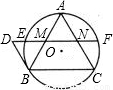
(2002•昆明)如图,已知:⊙O的弦AC、BD相交于点E,点A为 上一动点,当点A的位置在 时,△ABE∽△ACB.
上一动点,当点A的位置在 时,△ABE∽△ACB.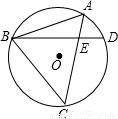
【答案】分析:看△ABE∽△ACB能得出什么条件,∠A是公共角,那么一定相等的对应角是∠ABE=∠ACB,那么弧AB=弧AD,因此此时点A是弧BD的中点.
解答:解:当点A是弧BD的中点时,△ABE∽△ACB,
理由如下:
∵点A是弧BD的中点
∴弧AB=弧AD
∴∠ABE=∠ACB
又∵∠A=∠A
∴△ABE∽△ACB.
点评:本题主要考查了相似三角形的判定及性质和圆周角定理的应用,弄清相似三角形中相等的对应角是解题的关键.
解答:解:当点A是弧BD的中点时,△ABE∽△ACB,
理由如下:
∵点A是弧BD的中点
∴弧AB=弧AD
∴∠ABE=∠ACB
又∵∠A=∠A
∴△ABE∽△ACB.
点评:本题主要考查了相似三角形的判定及性质和圆周角定理的应用,弄清相似三角形中相等的对应角是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 上一动点,当点A的位置在 时,△ABE∽△ACB.
上一动点,当点A的位置在 时,△ABE∽△ACB.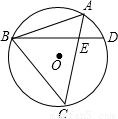
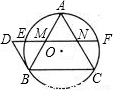
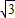 cm2,则此正六边形的边长为( )
cm2,则此正六边形的边长为( )