题目内容

如图所示，AB为⊙O的直径，D为 $数学公式$ 中点，连接BC交AD于E，DG⊥AB于G．
（1）求证：BD²=AD•DE；
（2）如果tanA= $数学公式$ ，DG=8，求DE的长．

（1）证明：连接BD．
∵D为 $\text{[math]}$ 中点，
∴ $\text{[math]}$ = $\text{[math]}$ ，
∴∠DAB=∠DBE，
又∵∠BDE=∠ADB，
∴△BDE∽△ADB，
∴BD：AD=DE：BD，
∴BD²=AD•DE；

（2）解：∵DG⊥AB于G，
∴∠AGD=90°．
∵AB为⊙O的直径，
∴∠ADB=90°．
在Rt△ADG中，∵tanA= $\text{[math]}$ ，∴ $\text{[math]}$ = $\text{[math]}$ ．
设DG=3k，则AG=4k，AD=5k，∴ $\text{[math]}$ = $\text{[math]}$ ．
又∵DG=8，∴AD= $\text{[math]}$ ．
在Rt△ADB中，tanA= 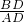$\text{[math]}$ = $\text{[math]}$ ，∴BD= $\text{[math]}$ AD=10．
∵BD²=AD•DE，
∴DE= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
分析：（1）连接BD，先由D为 $\text{[math]}$ 中点，根据圆心角、弧、弦的关系及圆周角定理得出 $\text{[math]}$ = $\text{[math]}$ ，∠DAB=∠DBE，又∠ADB公共，根据两角对应相等的两三角形相似得出△BDE∽△ADB，然后由相似三角形对应边成比例得出BD：AD=DE：BD，即为BD²=AD•DE；
（2）先在Rt△ADG中，由tanA= $\text{[math]}$ ，DG=8，求出AD= $\text{[math]}$ ，然后解Rt△ADB，求出BD=10，再根据（1）的结论BD²=AD•DE，即可求出DE的长．
点评：本题考查了圆心角、弧、弦的关系，圆周角定理，相似三角形的判定与性质，勾股定理，解直角三角形，综合性较强，有一定难度．