题目内容
附加题:(1)若一个角的补角是这个角的余角的3倍,则这个角是
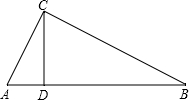
(2)在Rt△ABC中,∠ACB=90°,CD是AB边上的高,若AB=13,BC=12,AC=5,则CD=
分析:(1)设这个角是x,根据补角、余角可得关于x的方程,求解即可;
(2)根据直角三角形的面积既等于两直角边积的一半,也等于斜边乘以斜边上高的一半,得到相等关系,从而可求CD.
(2)根据直角三角形的面积既等于两直角边积的一半,也等于斜边乘以斜边上高的一半,得到相等关系,从而可求CD.
解答:解:(1)设这个角是x,根据题意得
180°-x=3(90°-x),
解得x=45°;
(2)∵S△ABC=
AC×BC=
AB×CD,
∴5×12=13CD,
∴CD=
.
故答案为:45°;
.
180°-x=3(90°-x),
解得x=45°;
(2)∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴5×12=13CD,
∴CD=
| 60 |
| 13 |
故答案为:45°;
| 60 |
| 13 |
点评:本题考查了三角形面积公式、余角和补角.解题的关键是知道直角三角形面积公式有两种计算方法.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目