题目内容
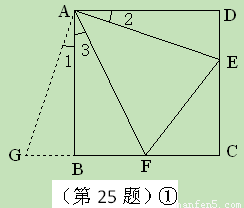
如图11,正方形ABCD的边长为5,点F为正方形ABCD内的点,△BFC经逆时针旋转后能与△BEA重合.
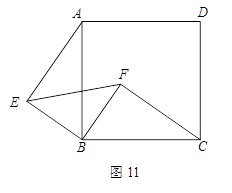
(1)旋转中心是哪一点?旋转了多少度?
(2)判断△BEF是怎样的三角形?并说明理由;
(3)若BE=3,FC=4,说明AE∥BF.
(1)旋转中心是点B,旋转了90°
(2)等腰直角三角形
(3)证明略
解析:(1)旋转中心是点B,旋转了90°.……………………(4分)
(2)△BEF是等腰直角三角形. 理由如下:
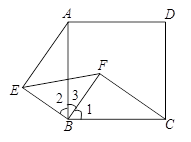
∵ △BFC经逆时针旋转后能与△BEA重合,
∴ ∠1=∠2,BF=BE.
∵ 四边形ABCD是正方形,
∴ ∠1+∠3=∠ABC=90°,
∴ ∠2+∠3=∠EBF=90°,
∴△BEF是等腰直角三角形. ………………………………(8分)
(3)在△BFC中,BF2+FC2=32+42=25=BC2,
∴ △BFC是直角三角形,∠BFC=90°.
∵ △BFC≌△BEA,
∴ ∠BEA =∠BFC =90°,
∴ BE⊥AE.
∵ BE⊥BF,
∴ AE∥BF. ………………………………(12分)
(注:用其它方法求解参照以上标准给分.)

练习册系列答案
相关题目
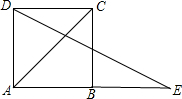 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E是( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E是( )| A、45° | B、22.5° | C、11.5° | D、40° |
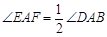 ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
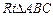 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=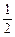 ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.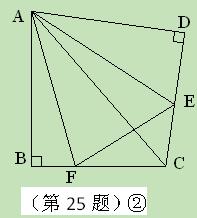
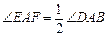 ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=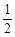 ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.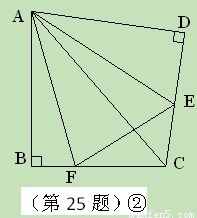
 ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).