题目内容
(1)已知:2x-y=10,求[(x2+y2)-(x-y)2+2y(x-y)]÷4y的值.
(2)分解因式(x+2)(x+4)+x2-4.
解:(1)原式=[x2+y2-x2+2xy-y2+2xy-2y2]÷4y=(4xy-2y2)÷4y=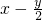
把y=2x-10代入上式得:
原式=x- =5;
=5;
(2)(x+2)(x+4)+x2-4
=(x+2)(x+4)+(x+2)(x-2)
=(x+2)[(x+4)+(x-2)]
=(x+2)(2x+2)
=2(x+2)(x+1);
分析:(1)利用整式的混合运算顺序分别进行计算即可;先去掉小括号,再进行合并,再根据多项式除以单项式的法则进行计算,再把2x-y=10代入,即可求出答案;
(2)利用提公因式法进行计算即可求出答案;先把x2-4进行因式分解,再提取公因式(x+2),即可求出答案;
点评:此题考查了整式的混合运算-化简求值,此题难度一般,解题时要注意整式的运算顺序;解题时要细心.
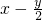
把y=2x-10代入上式得:
原式=x-
 =5;
=5;(2)(x+2)(x+4)+x2-4
=(x+2)(x+4)+(x+2)(x-2)
=(x+2)[(x+4)+(x-2)]
=(x+2)(2x+2)
=2(x+2)(x+1);
分析:(1)利用整式的混合运算顺序分别进行计算即可;先去掉小括号,再进行合并,再根据多项式除以单项式的法则进行计算,再把2x-y=10代入,即可求出答案;
(2)利用提公因式法进行计算即可求出答案;先把x2-4进行因式分解,再提取公因式(x+2),即可求出答案;
点评:此题考查了整式的混合运算-化简求值,此题难度一般,解题时要注意整式的运算顺序;解题时要细心.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知方程组
的解是正整数,则m的值为( )
|
| A、6 | B、4 | C、-4 | D、2 |