题目内容
【题目】已知k为任意实数，随着k的变化，抛物线y=x2﹣2（k﹣1）x+k2﹣3的顶点随之运动，则顶点运动时经过的路径与两条坐标轴围成图形的面积是（ ）
A. 1 B. 
C. 2 D. 
【答案】A
【解析】
利用配方法求出顶点坐标，得出顶点在直线y=2x﹣2上运动，由此即可解决问题．
∵y=x2﹣2（k﹣1）x+k2﹣3
=（x﹣k+1）2+k2﹣3﹣（k﹣1）2
=（x﹣k+1）2+2k﹣4
∴顶点的坐标为（k﹣1，2k﹣4）即[（k﹣1），2（k﹣1）﹣2]，∴顶点在直线y=2x﹣2上运动，易知直线y=2x﹣2交x轴于A（1，0），交y轴于B（0，﹣2），∴S△AOB=
×2×1=1，∴顶点运动时经过的路径与两条坐标轴围成图形的面积是1．
故选A．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
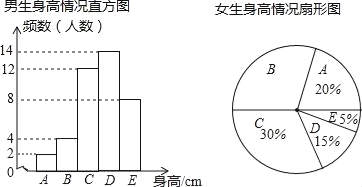
【题目】为了了解某校学生的身高状况，随机对该校男生、女生的身高进行抽样调查．已知抽取的样本中，男生、女生的人数相同，根据所得数据绘制如图所示的统计图表：
组别 | 身高（cm） |
A | x＜150 |
B | 150≤x＜155 |
C | 155≤x＜160 |
D | 160≤x＜165 |
E | x≥165 |
已知女生身高在A组的有8人，根据图表中提供的信息，回答下列问题：
（1）男生身高的中位数落在 组（填组别字母序号）；
（2）在样本中，身高在150≤x＜155之间的人数共有 人，身高人数最多的在 组（填组别序号）；
（3）已知该校共有男生400人、女生420人，请估计身高不足160cm的学生约有多少人？
