题目内容
如图,直线AB∥CD,直线EF与AB,CD分别交于点E,F,EC⊥EF,垂足为E,若∠1=60°,则∠2的度数为
| A.15° | B.30° | C.45° | D.60° |
B
解析试题分析:如图,∠3=∠1=60°(对顶角相等),
∵AB∥CD,EC⊥EF,
∴∠3+90°+∠2=180°,即60°+90°+∠2=180°。
解得∠2=30°。
故选B。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
如图,AB∥ED,∠ECF=70°,则∠BAF的度数为( )
| A.130° | B.110° | C.70° | D.20° |
下列命题中,是真命题的是( )
| A.同位角相等 | B.同旁内角互补 | C.内错角相等 | D.对顶角相等 |
观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是()
| A.21 | B.28 | C.36 | D.45 |
如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是
| A.40° | B.50° | C.60° | D.140° |
已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( )
| A.45° | B.60° | C.90° | D.180° |
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是【 】
| A.15° | B.20° | C.25° | D.30° |
如图,下列条件中能判定直线l1∥l2的是【 】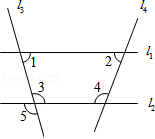
| A.∠1=∠2 | B.∠1=∠5 | C.∠1+∠3=180° | D.∠3=∠5 |
