题目内容
一个三角形的三边长分别为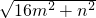 ,
, ,2
,2 ,(
,( >0),则这个三角形的面积是________.
>0),则这个三角形的面积是________.
5mn
分析:设三角形中,a=2 ,b=
,b=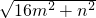 ,c=
,c= .作AD⊥BC于D,设CD=x.根据勾股定理,得到关于x的方程,再进一步根据勾股定理求得AD的长,从而求得三角形的面积.
.作AD⊥BC于D,设CD=x.根据勾股定理,得到关于x的方程,再进一步根据勾股定理求得AD的长,从而求得三角形的面积.
解答: 解:设三角形中,a=2
解:设三角形中,a=2 ,b=
,b=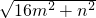 ,c=
,c= .
.
作AD⊥BC于D,设CD=x.
根据勾股定理,得
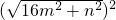 -x2=
-x2=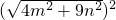 -
-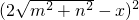 ,
,
解得
x=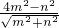 .
.
则这个三角形的面积是 ×2
×2 ×
×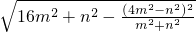 =
= =5mn.
=5mn.
点评:此题综合运用了二次根式的性质和勾股定理.
分析:设三角形中,a=2
 ,b=
,b=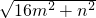 ,c=
,c= .作AD⊥BC于D,设CD=x.根据勾股定理,得到关于x的方程,再进一步根据勾股定理求得AD的长,从而求得三角形的面积.
.作AD⊥BC于D,设CD=x.根据勾股定理,得到关于x的方程,再进一步根据勾股定理求得AD的长,从而求得三角形的面积.解答:
 解:设三角形中,a=2
解:设三角形中,a=2 ,b=
,b=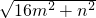 ,c=
,c= .
.作AD⊥BC于D,设CD=x.
根据勾股定理,得
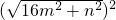 -x2=
-x2=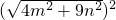 -
-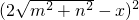 ,
,解得
x=
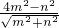 .
.则这个三角形的面积是
 ×2
×2 ×
×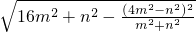 =
= =5mn.
=5mn.点评:此题综合运用了二次根式的性质和勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若一个三角形的三边长分别是15,20,25,则这个三角形最长的边上的高等于( )
| A、13 | B、12 | C、11 | D、10 |