题目内容
【题目】如图,四边形![]() ,
,![]() 、
、![]() 分别平分四边形的外角
分别平分四边形的外角![]() 和
和![]() ,设
,设![]() ,
,![]() .
.
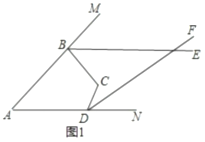
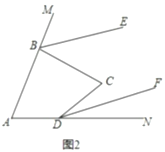
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图1,若![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,请写出
,请写出![]() 、
、![]() 所满足的等量关系式;
所满足的等量关系式;
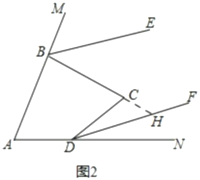
(3)如图2,若![]() ,判断
,判断![]() 、
、![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)120°;(2)![]() ;(3)平行,理由见解析
;(3)平行,理由见解析
【解析】
(1)根据四边形的内角和可求出∠ABC+∠ADC的度数,利用平角的定义即可得答案;(2)连接BD,根据角平分线的定义可得∠CBG+∠CDG=![]() (
(![]() ),在△BCD和△BGD中,利用三角形内角和定理即可得答案;(3)延长
),在△BCD和△BGD中,利用三角形内角和定理即可得答案;(3)延长![]() 交
交![]() 于
于![]() ,根据角平分线的定义可得∠CBE+∠CDH=
,根据角平分线的定义可得∠CBE+∠CDH=![]() (
(![]() ),根据外角性质可得
),根据外角性质可得![]() ,即可得出
,即可得出![]() ,根据
,根据![]() 可得
可得![]() ,根据平行线的判定定理即可得BE//DF.
,根据平行线的判定定理即可得BE//DF.
(1)∵四边形ABCD的内角和为(4-2)×180°=360°,![]()
∴![]() ,
,
∴![]() .
.
(2)![]()
理由:如图1,连接![]() ,
,
由(1)得![]() ,
,
∵![]() 、
、![]() 分别平分四边形的外角
分别平分四边形的外角![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
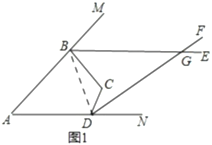
(3)平行,理由如下:
如图2,延长![]() 交
交![]() 于
于![]() ,
,
由(1)得![]() ,
,
∵![]() 、
、![]() 分别平分四边形的外角
分别平分四边形的外角![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目