题目内容
 如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,在此直角坐标系中画直线y=kx+2,若直线y=kx+2与⊙O相切,则k=________.
如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,在此直角坐标系中画直线y=kx+2,若直线y=kx+2与⊙O相切,则k=________.
- 或
或
分析:可设直线y=kx+2与x轴的交点坐标为B(a,0),根据勾股定理可用a表示出AB的长,再根据切线的性质和三角形的面积得到关于a的方程,解方程即可求得B点坐标,代入得到直线y=kx+2,得到关于k的方程,求解即可.
解答: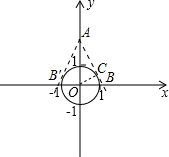 解:如图,过O点作OC⊥AB于C.
解:如图,过O点作OC⊥AB于C.
设直线y=kx+2与x轴的交点坐标为B(a,0),依题意有
OA=2,OB=|a|,
则AB= ,
,
则 ×2×|a|=
×2×|a|= ×1×
×1× ,
,
解得a=± ,
,
当a= 时,把B(
时,把B( ,0)代入y=kx+2,得
,0)代入y=kx+2,得 k+2=0,解得k=-
k+2=0,解得k=- ;
;
当a=- 时,把B(-
时,把B(- ,0)代入y=kx+2,得-
,0)代入y=kx+2,得- k+2=0,解得k=
k+2=0,解得k= .
.
故k=- 或
或 .
.
故答案为:- 或
或 .
.
点评:本题考查了一次函数和几何问题的综合应用,本题涉及的知识点有直线与坐标轴的交点坐标,勾股定理的应用,切线的性质和三角形的面积,解方程,综合性较强,注意分两种情况讨论求解.
 或
或
分析:可设直线y=kx+2与x轴的交点坐标为B(a,0),根据勾股定理可用a表示出AB的长,再根据切线的性质和三角形的面积得到关于a的方程,解方程即可求得B点坐标,代入得到直线y=kx+2,得到关于k的方程,求解即可.
解答:
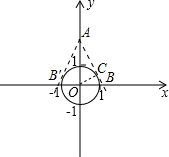 解:如图,过O点作OC⊥AB于C.
解:如图,过O点作OC⊥AB于C.设直线y=kx+2与x轴的交点坐标为B(a,0),依题意有
OA=2,OB=|a|,
则AB=
 ,
,则
 ×2×|a|=
×2×|a|= ×1×
×1× ,
,解得a=±
 ,
,当a=
 时,把B(
时,把B( ,0)代入y=kx+2,得
,0)代入y=kx+2,得 k+2=0,解得k=-
k+2=0,解得k=- ;
;当a=-
 时,把B(-
时,把B(- ,0)代入y=kx+2,得-
,0)代入y=kx+2,得- k+2=0,解得k=
k+2=0,解得k= .
.故k=-
 或
或 .
.故答案为:-
 或
或 .
.点评:本题考查了一次函数和几何问题的综合应用,本题涉及的知识点有直线与坐标轴的交点坐标,勾股定理的应用,切线的性质和三角形的面积,解方程,综合性较强,注意分两种情况讨论求解.

练习册系列答案
相关题目