题目内容
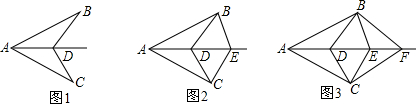
 如图①,已知AB∥CD,BP、DP分别平分∠ABD、∠BDC.
如图①,已知AB∥CD,BP、DP分别平分∠ABD、∠BDC.(1)∠BPD=
90
90
°;(2)如图②,将BD改为折线BED,BP、DP分别平分∠ABE、∠EDC,其余条件不变,若∠BED=150°,求∠BPD的度数:并进一步猜想∠BPD与∠BED之间的数量关系.
分析:(1)先根据平行线的性质得出∠ABD+∠BDC=∠180°,再根据角平分线的定义得出∠PBD+∠PDB的度数,由三角形内角和定理即可得出结论;
(2)连接BD,先根据∠BED=150°求出∠EBD+∠EDB的度数,再由平行线的性质得出∠ABD+∠CDB的度数,由角平分线的性质得出∠PBE+∠PDE的度数,根据∠BPD=180°-∠PBE-PDE-∠EBD-∠EDB即可得出结论.
(2)连接BD,先根据∠BED=150°求出∠EBD+∠EDB的度数,再由平行线的性质得出∠ABD+∠CDB的度数,由角平分线的性质得出∠PBE+∠PDE的度数,根据∠BPD=180°-∠PBE-PDE-∠EBD-∠EDB即可得出结论.
解答:解:(1)∵AB∥CD,
∴∠ABD+∠BDC=∠180°,
∵BP、DP分别平分∠ABD、∠BDC,
∴∠PBD+∠PDB=90°,
∴∠BPD=180°-90°=90°.
故答案为:90;
(2) 连接BD,
连接BD,
∵∠BED=150°,
∴∠EBD+∠EDB=30°,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
∵BP、DP分别平分∠ABE、∠EDC,
∴∠PBE=
∠ABE,∠PDE=
∠CDE,
∴∠PBE+∠PDE=
(180°-30°)=75°,
∴∠BPD=180°-∠PBE-PDE-∠EBD-∠EDB=75°.
猜想:∠BPD=
∠BED.
∴∠ABD+∠BDC=∠180°,
∵BP、DP分别平分∠ABD、∠BDC,
∴∠PBD+∠PDB=90°,
∴∠BPD=180°-90°=90°.
故答案为:90;
(2)
 连接BD,
连接BD,∵∠BED=150°,
∴∠EBD+∠EDB=30°,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
∵BP、DP分别平分∠ABE、∠EDC,
∴∠PBE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PBE+∠PDE=
| 1 |
| 2 |
∴∠BPD=180°-∠PBE-PDE-∠EBD-∠EDB=75°.
猜想:∠BPD=
| 1 |
| 2 |
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 证明下列各题.
证明下列各题. 完成说理过程并注明理由:
完成说理过程并注明理由: