题目内容
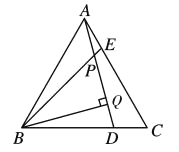
【题目】已知ABCD的周长为26，∠ABC=120°，BD为一条对角线，⊙O内切于△ABD，E，F，G为切点，已知⊙O的半径为
．求ABCD的面积．
【答案】20
【解析】
首先利用三边及⊙O的半径表示出平行四边形的面积，再根据题意求出AB+AD=13，然后利用切线的性质求出BD的长即可解答.
设⊙O分别切△ABD的边AD、AB、BD于点G、E、F；
平行四边形ABCD的面积为S；
则S=2S△ABD=2×
(AB·OE+BD·OF+AD·OG)=（AB+AD+BD）；
∵平行四边形ABCD的周长为26，
∴AB+AD=13，
∴S=(13+BD)；连接OA；
由题意得：∠OAE=30°，
∴AG=AE=3；同理可证DF=DG，BF=BE；
∴DF+BF=DG+BE=13﹣3﹣3=7，
即BD=7，
∴S=（13+7）=20．
即平行四边形ABCD的面积为20．
练习册系列答案
相关题目
