题目内容
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=__________时,四边形MENF是正方形(只写结论,不需证明).

(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,
∵M是AD的中点,
∴AM=DM,
在△ABM和△DCM中, ,
,
∴△ABM≌△DCM(SAS),
∴BM=CM;
(2)解:四边形MENF是菱形;理由如下:
∵E、N、F分别是线段BM、BC、CM的中点,
∴EN是△BCM的中位线,
∴EN= CM=FM,EN∥FM,
CM=FM,EN∥FM,
∴四边形MENF是平行四边形,
同理:NF是△BCM的中位线,
∴N F=
F= BM,
BM,
∵BM=CM,
∴EN=NF,
∴四边形MENF是菱形;
(3)解:当AD:AB=2:1时,四边形MENF是正方形;理由如下:
∵AD:AB=2:1,M是AD的中点,
∴AB=AM,
∴△ABM是等腰直角三角形,
∴∠AMB=45°,
同理:∠DMC=45°,
∴∠EMF=180°﹣45°﹣45°=90°,
由(2)得:四边形MENF是菱形,
∴四边形MENF是正方形;
故答案为:2:1.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
 中的x与y都扩大为原来的10倍,那么这个代数式的值( )
中的x与y都扩大为原来的10倍,那么这个代数式的值( )
 成如下两幅不完整的统计图,请根据图中信息解答下列问题:
成如下两幅不完整的统计图,请根据图中信息解答下列问题:
 =
= B.
B. =
= C.
C. D.
D. (a≠0)
(a≠0) 的值 ①等于0?②小于0?
的值 ①等于0?②小于0? 的图象在( )
的图象在( ) +(x﹣3)﹣2中自变量x的取值范围是__________.
+(x﹣3)﹣2中自变量x的取值范围是__________.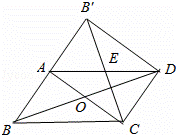
 中,自变量x的取值范围是
中,自变量x的取值范围是